question_answer

A worker piles up sand onto a circular area of radius R. No sand is to spill onto the surrounding area. The coefficient of friction of sand on sand is \[\mu \]. The greatest volume of the sand that can be stored in the manner is

A) \[\frac{\pi \mu {{R}^{3}}}{3}\]

B) \[\frac{\pi \mu {{R}^{3}}}{6}\]

C) \[\frac{\pi {{R}^{3}}}{3\mu }\]                        

D) None       

Correct Answer: A

Solution :

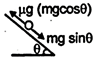
The weight component of a particle is balanced by static friction \[mg\sin \theta =\mu (mg\cos \theta )\] \[\mu =\tan \theta =\frac{h}{R}\]

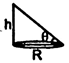
So \[h=\mu R\]

Volume \[=\frac{1}{3}\pi {{R}^{2}}h=\frac{1}{3}\pi {{R}^{2}}(\mu R)=\frac{\pi \mu {{R}^{3}}}{3}\]