question_answer

Two plane mirrors of length L are separated by distance L and a man \[{{M}_{2}}\] is standing at distance L from the connecting line of mirrors as shown in figure. A man \[{{M}_{1}}\] is walking in a straight line at distance 2L parallel to mirrors at speed u, then man \[{{M}_{2}}\] at O will be able to see image of \[{{M}_{1}}\] for time:

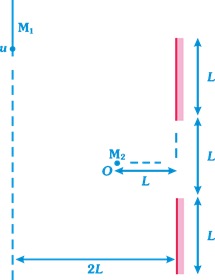
A) \[\frac{4L}{u}\]

B) \[\frac{3L}{u}\]

C) \[\frac{6L}{u}\]

D)  \[\frac{9L}{u}\]

Correct Answer: C

Solution :

[c]

\[\tan \theta =\frac{PR}{OR}=\frac{AC}{PC}\]\[\Rightarrow \]            \[\frac{3L/2}{L}=\frac{AC}{2L}\,\,\,\,\,\Rightarrow \,\,\,AC=3L\]

\[\tan \alpha =\frac{QR}{OR}=\frac{BD}{DQ}\]\[\Rightarrow \]            \[BD=\frac{L/2}{L}\times 2L=L\]

\[\therefore \]      \[AB=AD-BD=(3L+L)-L=3L\]

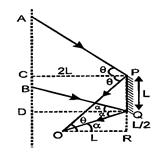From A to B observer can observe \[{{M}_{1}}\]

Making similar diagram for lower mirror

Total visible distance \[=3L+3L=6L\]

Total time \[=\frac{6L}{u}\]