| An ideal gas can be expanded from an initial state to a certain volume through two different processes |
| (i) \[P{{V}^{2}}=\] constant and |
| (ii) \[P=K{{V}^{2}}\] where K is a positive constant. Then |
A) Final temperature in (i) will be greater then in (ii)
B) Final temperature in (ii) will be equal to (i)
C) Total heat given to the gas in (i) case is greater than in (ii)
D) Total heat given to the gas in (ii) case is greater than in (i)
Correct Answer: D
Solution :
| [d] From equation \[PV=nRT\] |
| \[{{P}_{C}}<{{P}_{B}},\,\,{{V}_{C}}={{V}_{B}}\] and \[{{T}_{C}}-{{T}_{A}}\] |
| \[{{W}_{AB}}>{{W}_{AC}}\] \[({{T}_{B}}-{{T}_{A}})>{{T}_{C}}-{{T}_{A}}\] |
| So by 1st law |
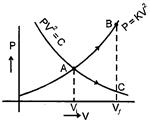 |
| \[Q=\Delta U+W\] |
| \[Q=\frac{1}{2}nRT\,\Delta T+W\] |
| \[{{Q}_{AB}}>{{Q}_{AC}}\] |
You need to login to perform this action.
You will be redirected in
3 sec
