-
question_answer1) If \[x=-\frac{1}{2},\] is a solution of the quadratic equation \[3{{x}^{2}}+2kx-3=0\]find the value of k.
View Answer play_arrow
-
question_answer2) The tops of two towers of height x and y, standing on level ground, subtend angles of \[30{}^\circ \] and \[60{}^\circ \] respectively at the centre of the line joining their feet, then find \[x:y\].
View Answer play_arrow
-
question_answer3) A letter of English alphabet is chosen at random. Determine the probability that the chosen letter is a consonant.
View Answer play_arrow
-
question_answer4)
| In Fig. 1, PA and PB are tangents to the circle with centre O such that \[\angle APB=50{}^\circ \], Write the measure of\[\angle OAB\]. |
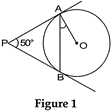 |
View Answer play_arrow
-
question_answer5)
| In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If \[\angle AOQ=58{}^\circ \], find \[\angle ATQ\]. |
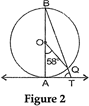 |
View Answer play_arrow
-
question_answer6)
| Solve the following quadratic equation for x: |
| \[4{{x}^{2}}-4{{a}^{2}}x+({{a}^{4}}-{{b}^{4}})=0\]. |
View Answer play_arrow
-
question_answer7) From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
View Answer play_arrow
-
question_answer8) Find the middle term of the A.P. 6, 13, 20, ??., 216.
View Answer play_arrow
-
question_answer9) If \[A\,(5,2),\text{ }B\,(2,-2)\] and \[C(-2,t)\] are the vertices of a right angled triangle with \[\angle B=90{}^\circ \]. then find the value of t.
View Answer play_arrow
-
question_answer10) Find the ratio in which the point \[P\left( \frac{3}{4},\frac{5}{12} \right)\] divides the line segment joining the points \[A\left( \frac{1}{2},\frac{3}{2} \right)\] and \[B(2,-5)\].
View Answer play_arrow
-
question_answer11) Find the area of the triangle ABC with \[A\,(1,-4)\] and mid-points of sides through A being \[(2,-1),\] and \[(0,-1)\].
View Answer play_arrow
-
question_answer12) Find that non-zero value of fc, for which the quadratic equation \[k{{x}^{2}}+1-2(k-1)x+{{x}^{2}}=0\] has equal roots. Hence find the roots of the equation.
View Answer play_arrow
-
question_answer13) The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is \[45{}^\circ \]. If the tower is 30 m high, find the height of the building.
View Answer play_arrow
-
question_answer14)
| Two different dice are rolled together. Find the probability of getting: |
| (i) the sum of numbers on two dice to be 5. |
| (ii) even numbers on both dice. |
View Answer play_arrow
-
question_answer15) If \[{{S}_{n}}\], denotes the sum of first n terms of an A.P, prow that \[{{S}_{12}}=3({{S}_{8}}-{{S}_{4}})\]
View Answer play_arrow
-
question_answer16)
| In Fig. 3, APB and AQO are semicircles, and \[AO=OB\]. If the perimeter of the figure is 40 cm, find the area of the shaded region. \[\left[ \text{Use}\,\pi =\frac{22}{7} \right]\] |
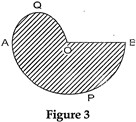 |
View Answer play_arrow
-
question_answer17)
| In Fig. 4, from the top of a solid cone of height 12 cm base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. \[\left[ \text{Use}\,\pi =\frac{22}{7}\text{and}\,\sqrt{5}=2.236 \right]\] |
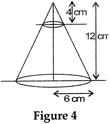 |
View Answer play_arrow
-
question_answer18) A solid wooden toy is in the form of hemisphere surmounted by a cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is \[166\frac{5}{6}c{{m}^{3}}\]. Find the height of the toy. Also, find the cost of painting hemispherical part of the toy at the rate of \[Rs.\,\,10\,\,per\,\,c{{m}^{2}}\]. \[\left[ \text{Use}\,\,\pi =\frac{22}{7} \right]\]
View Answer play_arrow
-
question_answer19)
| In Fig. 5, from a cuboidal solid metallic block, of dimensions \[15\text{ }cm\times 10\text{ }cm\times 5\text{ }cm\], a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block. \[\left[ \text{Use}\,\pi =\frac{22}{7} \right]\] |
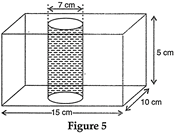 |
View Answer play_arrow
-
question_answer20)
| In Fig. 6, find the area of the shaded region [Use\[\pi =3.14\]] |
 |
View Answer play_arrow
-
question_answer21) The numerator of a fraction is 3 less than its denominator. If 2 is added to both the numerator and the denominator, then the sum of the new fraction and original fraction is \[\frac{29}{20}\]. Find the original fraction.
View Answer play_arrow
-
question_answer22)
| Ramkali required Rs. 2500 after 12 weeks to send her daughter to school. She saved Rs. 100 in the first week and increased her weekly saving by Rs. 20 every week. Find whether she will be able to send her daughter to school after 12 weeks. |
| What value is generated in the above situation? |
View Answer play_arrow
-
question_answer23)
| Solve for x: |
| \[\frac{2}{x+1}+\frac{3}{2(x-2)}=\frac{23}{5x},x\ne 0,-1,2\] |
View Answer play_arrow
-
question_answer24) Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
View Answer play_arrow
-
question_answer25)
| In Fig. 7, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that \[\angle RPQ=30{}^\circ \]. A chord RS is drawn parallel to the tangent PQ. Find \[\angle RQS\]. |
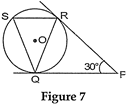 |
View Answer play_arrow
-
question_answer26) Construct a triangle ABC with \[BC=7\text{ }cm,\text{ }\angle B=60{}^\circ \] and \[AB=6\text{ }cm\]. Construct another triangle whose sides are \[\frac{3}{4}\] times the corresponding side of \[\Delta \,ABC\].
View Answer play_arrow
-
question_answer27) From a point P on the ground the angle of elevation of the top of a tower is \[30{}^\circ \] and that of the top of a flag staff fixed on the top of the tower, is \[60{}^\circ \]. If the length of the flag staff is 5 m, find the height of the tower.
View Answer play_arrow
-
question_answer28)
| A box contains 20 cards numbered from 1 to 20. A card is drawn at random from the box. Find the probability that the number on the drawn card is: |
| (i) divisible by 2 or 3 |
| (ii) a prime number |
View Answer play_arrow
-
question_answer29) If \[A(-4,8),\text{ }B(-3,-4),\text{ }C(0,-5)\] and \[D(5,6)\]are the vertices of a quadrilateral ABCD, find its area.
View Answer play_arrow
-
question_answer30) A well of diameter 4 m is dug 14 m deep. The earth taken out is spread evenly all around the well to form a 40 cm high embankment. Find the width of the embankment.
View Answer play_arrow
-
question_answer31) Water is flowing at the rate of 2.52 km/h through a cylindrical pipe into a cylindrical tank, the radius of whose base is 40 cm. If the increase in the level of water in the tank, in half an hour is 3/15 m, find the internal diameter of the pipe.
View Answer play_arrow







