-
question_answer1) In \[\Delta \,DEW,AB\parallel EW\]. If \[AD=4cm,\,\,DE\,=12cm\] and \[DW=24\text{ }cm\] , then find the of \[DB\].
View Answer play_arrow
-
question_answer2) If \[\Delta \text{ }ABC\] is right angled at By what is the value of \[\sin \,(A+C)\].
View Answer play_arrow
-
question_answer3) If \[\sqrt{3}\text{ }sin\text{ }\theta =cos\text{ }\theta \], find the value of \[\frac{3\,{{\cos }^{2}}\theta +2\,\cos \theta }{3\,\cos \theta +2}\].
View Answer play_arrow
-
question_answer4)
| From the following frequency distribution, find the median class: |
| Cost of living index | 1400 ? 1550 | 1550 ? 1700 | 1700 ? 1850 | 1850 ? 2000 |
| Number of weeks | 8 | 15 | 21 | 8 |
View Answer play_arrow
-
question_answer5) Show that \[3\sqrt{7}\] is an irrational number.
View Answer play_arrow
-
question_answer6) Explain why \[(17\times 5\times 11\times 3\times 2+2\times 11)\] is a composite number?
View Answer play_arrow
-
question_answer7)
| Find whether the following pair of linear equations is consistent or inconsistent: |
| \[3x+2y=8\] |
| \[6x-4y=9\] |
View Answer play_arrow
-
question_answer8) X and Y are points on the sides AB and AC respectively of a triangle ABC such that \[\frac{AX}{AB},AY=2\,cm\] and \[YC=6\,cm\]. Find whether \[XY\parallel BC\] or not.
View Answer play_arrow
-
question_answer9)
| Prove the following identity: |
| \[\frac{{{\sin }^{3}}\theta +{{\cos }^{2}}\theta }{\sin \theta +cos\theta }=1-\sin \theta .\cos \theta \]. |
View Answer play_arrow
-
question_answer10)
| Show that the mode of the series obtained by combining the two series \[{{S}_{1}}\] and \[{{S}_{2}}\] given below is different from that of \[{{S}_{1}}\] and \[{{S}_{2}}\] taken separately: |
| \[{{S}_{1}}:3,\,\,5,\,\,8,\,\,8,\,\,9,\,\,12,\,\,13,\,\,9,\,\,9\] |
| \[{{S}_{2}}:7,\,\,4,\,\,7,\,\,8,\,\,7,\,\,8,\,\,13\] |
View Answer play_arrow
-
question_answer11) The length, breadth and height of a room are 8 m 50 cm, 6 m 25 cm and 4 m 75 cm respectively. Find the length of the longest rod that can measure the dimensions of the room exactly.
View Answer play_arrow
-
question_answer12)
| Solve by elimination: |
| \[3x-y=7\] |
| \[2x+5y+1=0\] |
View Answer play_arrow
-
question_answer13) Find a quadratic polynomial, the sum and product of whose zeroes are 0 and \[-\frac{3}{5}\] respectively. Hence find the zeroes.
View Answer play_arrow
-
question_answer14) The sum of the digits of a two digit number is 8 and the difference between the number and that formed by reversing the digits is 18. Find the number.
View Answer play_arrow
-
question_answer15)
| In given figure, \[EB\bot AC,\text{ }BG\bot AE\] and \[CF\bot AE\] Prove that: |
| (i)\[\Delta \,ABG\sim \Delta \,DCB\] |
| (ii) \[\frac{BC}{BD}=\frac{BE}{BA}\] |
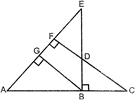 |
View Answer play_arrow
-
question_answer16) In triangle \[ABC\], if \[AP\bot BC\] and \[A{{C}^{2}}=B{{C}^{2}}-A{{B}^{2}}\], then prove that \[P{{A}^{2}}=PB\times CP\].
View Answer play_arrow
-
question_answer17) If \[\sin \theta =\frac{12}{13},0{}^\circ <\theta <90{}^\circ ,\], find the value of: \[\frac{{{\sin }^{2}}\theta -{{\cos }^{2}}\theta }{2\sin \theta .\cos \theta }\times \frac{1}{{{\tan }^{2}}\theta }\]
View Answer play_arrow
-
question_answer18) If \[sec\theta +tan\theta =p\], prove that \[\sin \theta =\frac{{{p}^{2}}-1}{{{p}^{2}}+1}\]
View Answer play_arrow
-
question_answer19)
| Find the mean of the following distribution by Assumed Mean Method: |
| Class interval | Frequency |
| 10 ? 20 | 8 |
| 20 ? 30 | 7 |
| 30 ? 40 | 12 |
| 40 ? 50 | 23 |
| 50 ? 60 | 11 |
| 60 ? 70 | 13 |
| 70 ? 80 | 8 |
| 80 ? 90 | 6 |
| 90 ? 100 | 12 |
View Answer play_arrow
-
question_answer20) The average score of boys in the examination of a school is 71 and that of the girls is 73. The average score of the school in the examination is 71.8. Find the ratio of number of boys in the number of girls who appeared in the examination.
View Answer play_arrow
-
question_answer21) Find HCF of numbers 134791, 6341 and 6339 by Euclid?s division algorithm.
View Answer play_arrow
-
question_answer22)
| Draw the graph of the following pair of linear equations: |
| \[x+3y=6\] and \[2x-3y=2\] |
| Find the ratio of the areas of the two triangles formed by first line, \[x=0,\text{ }y=0\] and second line, \[x=0,\text{ }y=0\]. |
View Answer play_arrow
-
question_answer23) If the polynomial \[({{x}^{4}}+2{{x}^{3}}+8{{x}^{2}}+12x+18)\]is divided by another polynomial \[({{x}^{2}}+5)\], the remainder comes out to be \[(px+q)\], find the values of p and q.
View Answer play_arrow
-
question_answer24) What must be subtracted from \[p(x)=8{{x}^{4}}+14{{x}^{3}}-2{{x}^{2}}+8x-12\] so that \[4{{x}^{2}}+3x-2\] is factor of \[p(x)\]? This question was given to group of students for working together. Do you think teacher should promote group work?
View Answer play_arrow
-
question_answer25) Prove ?If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio?.
View Answer play_arrow
-
question_answer26)
| In the given figure, \[AD=3cm,\,\,AE=5cm,\,\,BD=4cm,\,\,CE=4cm,\,\,CF=2cm,\,\,BF=2.5cm\], then find the pair of parallel lines and hence their lengths. |
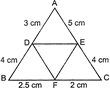 |
View Answer play_arrow
-
question_answer27) If tan\[(A+B)=\sqrt{3}\] and tan\[(A-B)=\frac{1}{\sqrt{3}}\] , where\[0<A+B<90{}^\circ ,\text{ }A>B\], find A and B. Also calculate\[\tan \text{ }A.\text{ }\sin \text{ }(A+B)+\cos \text{ }A.\text{ }\tan \text{ }(A-B)\].
View Answer play_arrow
-
question_answer28) Prove that: \[(1+cot\text{ }A+tan\text{ }A).\text{(}sin\text{ }A-cos\text{ }A)\]\[=\frac{{{\sec }^{3}}A-\cos e{{c}^{3}}A}{{{\sec }^{2}}A.\cos e{{c}^{2}}A}\]
View Answer play_arrow
-
question_answer29) Prove the identity: \[\frac{\sin A+\cos A}{\sin A-\cos A}+\frac{\sin A-\cos A}{\sin A+\cos A}=\frac{2}{1-2{{\cos }^{2}}A}\]
View Answer play_arrow
-
question_answer30)
| The following table gives the daily income of 50 workers of a factory. Draw both types (?less than type? and ?greater than type?) ogives. |
| Daily income in Rs. | No. of workers |
| 100 ? 120 | 12 |
| 120 ? 140 | 14 |
| 140 ? 160 | 8 |
| 160 ? 180 | 6 |
| 180 ? 200 | 10 |
View Answer play_arrow
-
question_answer31)
| In a class test, marks obtained by 120 students are given in the following frequency distribution. If it is given that mean is 59, find the missing frequencies x and y. |
| Marks | No. of students |
| 0 ? 10 | 1 |
| 10 ? 20 | 3 |
| 20 ? 30 | 7 |
| 30 ? 40 | 10 |
| 40 ? 50 | 15 |
| 50 ? 60 | x |
| 60 ? 70 | 9 |
| 70 ? 80 | 27 |
| 80 ? 90 | 18 |
| 90 ? 100 | y |
View Answer play_arrow


