A) Statement-1 is true, statement-2 is true; statement-2 is a correct explanation for Statement-1.
B) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for statement-1
C) Statement-1 is true, Statement-2 is false.
D) Statement-1 is false, Statement-2 is true.
Correct Answer: B
Solution :
\[f(x)=\left\{ \begin{matrix} \frac{\tan x}{x} & x\ne 0 \\ 1 & x=0 \\ \end{matrix} \right.\] In right neighborhood of '0' tan x > x \[\frac{\tan x}{x}>1\]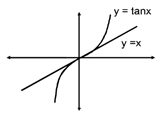 In left neighborhood of '0' tan x < x \[\frac{\tan x}{x}>1\] as (x < 0) at x = 0, f (x) = 1 \[\Rightarrow \] x = 0 is point of minima so statement 1 is true. statement 2 obvious
In left neighborhood of '0' tan x < x \[\frac{\tan x}{x}>1\] as (x < 0) at x = 0, f (x) = 1 \[\Rightarrow \] x = 0 is point of minima so statement 1 is true. statement 2 obvious
You need to login to perform this action.
You will be redirected in
3 sec
