A) \[2y-3x=0\]
B) \[y=\frac{6}{x}\]
C) \[{{x}^{2}}+{{y}^{2}}=13\]
D) \[{{\left( \frac{x}{2} \right)}^{2}}+{{\left( \frac{y}{3} \right)}^{2}}=2\]
Correct Answer: B
Solution :
\[Y-y=\frac{dy}{dx}(X-x)\] X-intercept is \[\left( x-\frac{y}{dy/dx},0 \right)\] Y=intercept is \[\left( 0,y-\frac{xdy}{dx} \right)\] According to statement \[x-\frac{y}{dy/dx}=2x\]and\[y-\frac{xdy}{dx}=2y\] \[\frac{\frac{-y}{dy}}{dx}=x\] \[\frac{-xdy}{dx}=y\] \[\frac{dx}{x}+\frac{dy}{y}=0\] \[\ell ny=-\ell nx+\ell nc\] \[y=\frac{c}{x}\Rightarrow c=6\] Hence\[y=\frac{6}{x}\]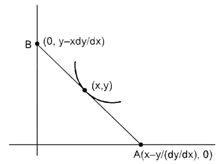
You need to login to perform this action.
You will be redirected in
3 sec
