A) 0
B) 1
C) 2
D) \[-2\]
Correct Answer: A
Solution :
Since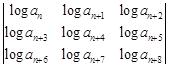
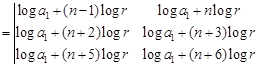
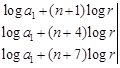 Applying,
Applying,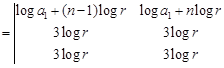
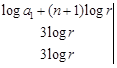 (since, two rows are identical) Alternate Solution Since,
(since, two rows are identical) Alternate Solution Since,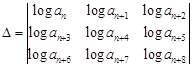
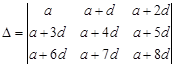 where, a and c/ are the first term and common difference of an AP. Applying
where, a and c/ are the first term and common difference of an AP. Applying 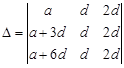 (since, two columns are identical)
(since, two columns are identical)
You need to login to perform this action.
You will be redirected in
3 sec
