A) \[120{}^\circ \]
B) \[45{}^\circ \]
C) \[60{}^\circ \]
D) \[90{}^\circ \]
Correct Answer: A
Solution :
Let the magnitude of two velocities be\[u\]. We know that, \[R=\sqrt{{{u}^{2}}+{{u}^{2}}+2{{u}^{2}}\cos \theta }\] \[R=\sqrt{2u}\sqrt{1+\cos \theta }\] \[R=2u\,\,\cos \frac{\theta }{2}\]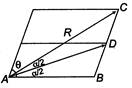 We know that by angle bisector theorem. \[\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow \frac{u}{2u\cos \frac{\theta }{2}}=1\] \[\Rightarrow \]\[\cos \frac{\theta }{2}=\frac{1}{2}=\cos \frac{\pi }{3}\] \[\Rightarrow \]\[\theta ={{120}^{o}}\]
We know that by angle bisector theorem. \[\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow \frac{u}{2u\cos \frac{\theta }{2}}=1\] \[\Rightarrow \]\[\cos \frac{\theta }{2}=\frac{1}{2}=\cos \frac{\pi }{3}\] \[\Rightarrow \]\[\theta ={{120}^{o}}\]
You need to login to perform this action.
You will be redirected in
3 sec
