A) \[\sqrt{\frac{{{x}^{3}}}{8}}\]
B) \[\frac{1}{2}{{x}^{2}}\]
C) \[\pi {{x}^{2}}\]
D) \[\frac{3}{2}{{x}^{2}}\]
Correct Answer: B
Solution :
The area of isosceles triangle is maximum when it is right angled triangle and then use area of\[\Delta =\frac{1}{2}\times b\times h\] Given that \[AB=AC=x\]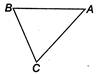 We know that area of isosceles triangle is maximum, if it is right angled triangle. \[\therefore \]Maximum area of triangle \[=\frac{1}{2}{{x}^{2}}\] Alternate Solution
We know that area of isosceles triangle is maximum, if it is right angled triangle. \[\therefore \]Maximum area of triangle \[=\frac{1}{2}{{x}^{2}}\] Alternate Solution 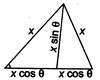 \[\therefore \]Area\[=\frac{1}{2}(2x\,\cos \theta )(x\sin \theta )\] \[=\frac{1}{2}{{x}^{2}}\sin 2\theta \] \[\therefore \]\[{{(Area)}_{\max }}=\frac{1}{2}{{x}^{2}}\]
\[\therefore \]Area\[=\frac{1}{2}(2x\,\cos \theta )(x\sin \theta )\] \[=\frac{1}{2}{{x}^{2}}\sin 2\theta \] \[\therefore \]\[{{(Area)}_{\max }}=\frac{1}{2}{{x}^{2}}\]
You need to login to perform this action.
You will be redirected in
3 sec
