A) \[(3,\infty )\]
B) \[\left( \frac{1}{2},3 \right)\]
C) \[\left( -3,-\frac{1}{2} \right)\]
D) \[\left( 0,\frac{1}{2} \right)\]
Correct Answer: B
Solution :
The graph of equations\[x-2y=0\]and\[3x-y=0\]is as shown in the figure. Since, given point \[(a,\,\,{{a}^{2}})\] lies in the shaded region.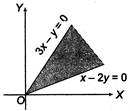 Since, \[x>0\Rightarrow a>0\] ...(i) From given condition, \[{{a}^{2}}-\frac{a}{2}>0\] \[\Rightarrow \] \[a\left( a-\frac{1}{2} \right)>0\] \[\Rightarrow \]\[a<0\]or \[a>\frac{1}{2}\] ...(ii) Also, \[{{a}^{2}}-3a<0\] \[\Rightarrow \]\[a(a-3)<0\] \[\Rightarrow \]\[a\in (0,3)\] ...(iii) From Eqs. (i), (ii) and (iii). we get \[a\in \left( \frac{1}{2},3 \right)\]
Since, \[x>0\Rightarrow a>0\] ...(i) From given condition, \[{{a}^{2}}-\frac{a}{2}>0\] \[\Rightarrow \] \[a\left( a-\frac{1}{2} \right)>0\] \[\Rightarrow \]\[a<0\]or \[a>\frac{1}{2}\] ...(ii) Also, \[{{a}^{2}}-3a<0\] \[\Rightarrow \]\[a(a-3)<0\] \[\Rightarrow \]\[a\in (0,3)\] ...(iii) From Eqs. (i), (ii) and (iii). we get \[a\in \left( \frac{1}{2},3 \right)\]
You need to login to perform this action.
You will be redirected in
3 sec
