A) \[m>3\]
B) \[-1<m<3\]
C) \[1<m<4\]
D) \[-2<m<0\]
Correct Answer: B
Solution :
Method I Given equation is\[{{x}^{2}}-2mx+{{m}^{2}}-1\]. Since, both roots are real and greater than -2 and less than 4. i.e., \[-2<x<4\] \[\Rightarrow \] \[-2<\frac{-b\pm \sqrt{D}}{2a}<4\]\[\Rightarrow \] \[-2<m\pm 1<4\] [\[\because \]\[D=4{{m}^{2}}-4{{m}^{2}}+4\]] \[\Rightarrow \] \[-2<m\pm 1<4\] Either \[-3<m<3\] ...(i) and \[-1<m<5\] ...(ii) The common set of values of 'm' satisfying the condition given is \[-1<\text{ }m<\text{ }3\] Method II Since, both roots of equation \[{{x}^{2}}-2mx+{{m}^{2}}-1=0\]are greater than -2 but less than 4. \[\therefore \] \[D\ge 0\] \[\Rightarrow \]\[4{{m}^{2}}-4{{m}^{2}}+4\ge 0\Rightarrow m\in R\] ...(i) and \[-2<\frac{-b}{2a}<4\Rightarrow -2<\left( \frac{2m}{2.1} \right)<4\] \[\Rightarrow \]\[-2<m<4\] ...(ii)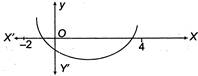 Also, \[f(4)>0\Rightarrow 16-8m+{{m}^{2}}-1>0\] \[\Rightarrow \] \[{{m}^{2}}-8m+15>0\] \[\Rightarrow \] \[(m-3)(m-5)>0\] \[\Rightarrow \] \[-\infty <m<3\] and \[5<m<\infty \] ...(iii) Also,\[f(-2)>0\Rightarrow 4+4m+{{m}^{2}}-1>0\] \[\Rightarrow \]\[{{m}^{2}}+4m+3>0\] \[\Rightarrow \]\[(m+3)(m+1)>0\] \[\Rightarrow \] \[-\infty <m<-3\]and\[-1<m<\infty \] ...(iv) From Eqs. (i), (ii), (iii) and (iv), we get m lies between -1 and 3
Also, \[f(4)>0\Rightarrow 16-8m+{{m}^{2}}-1>0\] \[\Rightarrow \] \[{{m}^{2}}-8m+15>0\] \[\Rightarrow \] \[(m-3)(m-5)>0\] \[\Rightarrow \] \[-\infty <m<3\] and \[5<m<\infty \] ...(iii) Also,\[f(-2)>0\Rightarrow 4+4m+{{m}^{2}}-1>0\] \[\Rightarrow \]\[{{m}^{2}}+4m+3>0\] \[\Rightarrow \]\[(m+3)(m+1)>0\] \[\Rightarrow \] \[-\infty <m<-3\]and\[-1<m<\infty \] ...(iv) From Eqs. (i), (ii), (iii) and (iv), we get m lies between -1 and 3
You need to login to perform this action.
You will be redirected in
3 sec
