A) \[\frac{(AB)(AC)}{AB+AC}\]
B) \[\frac{1}{AB}+\frac{1}{AC}\]
C) \[\frac{1}{AD}\]
D) \[\frac{A{{B}^{2}}+A{{C}^{2}}}{(A{{B}^{2}}){{(AC)}^{2}}}\]
Correct Answer: C
Solution :
Let \[|BC|=l\] In \[\Delta ABC,\]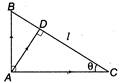 \[l=\sqrt{A{{B}^{2}}+A{{C}^{2}}}\] and \[\tan \theta =\frac{AB}{AC}\] \[\Rightarrow \] \[\sin \theta =\frac{AB}{l}\]and \[\cos \theta =\frac{AC}{l}\] \[\therefore \]Resultant vector \[=\frac{1}{AB}\hat{i}+\frac{1}{AC}\hat{j}=\left( \frac{1}{l\sin \theta }\hat{i}+\frac{1}{l\cos \theta }\hat{j} \right)\] \[=k\,AD\] Now,\[AD=AC\text{ }\sin \theta =l\,\cos \theta \sin \theta \] \[=\frac{AB.AC}{l}\] ...(i) Magnitude of resultant vector \[=\sqrt{\frac{1}{{{t}^{2}}}\left( \frac{1}{{{\sin }^{2}}\theta }+\frac{1}{{{\cos }^{2}}\theta } \right)}\] \[=\frac{l}{(AB)(AC)}=\frac{1}{AD}\] [from Eq.(i)]
\[l=\sqrt{A{{B}^{2}}+A{{C}^{2}}}\] and \[\tan \theta =\frac{AB}{AC}\] \[\Rightarrow \] \[\sin \theta =\frac{AB}{l}\]and \[\cos \theta =\frac{AC}{l}\] \[\therefore \]Resultant vector \[=\frac{1}{AB}\hat{i}+\frac{1}{AC}\hat{j}=\left( \frac{1}{l\sin \theta }\hat{i}+\frac{1}{l\cos \theta }\hat{j} \right)\] \[=k\,AD\] Now,\[AD=AC\text{ }\sin \theta =l\,\cos \theta \sin \theta \] \[=\frac{AB.AC}{l}\] ...(i) Magnitude of resultant vector \[=\sqrt{\frac{1}{{{t}^{2}}}\left( \frac{1}{{{\sin }^{2}}\theta }+\frac{1}{{{\cos }^{2}}\theta } \right)}\] \[=\frac{l}{(AB)(AC)}=\frac{1}{AD}\] [from Eq.(i)]
You need to login to perform this action.
You will be redirected in
3 sec
