from the horizontal. A 150 pound man is 4 ft from the top of the ladder. A horizontal force is needed to keep it from slipping. Choose the correct magnitude of force from the following:
A) 17.3 pound
B) 100 pound
C) 120 pound
D) 150 pound
Correct Answer: A
Solution :
Key Idea: The net moment about point of contact between ground and ladder should be zero. Let (as shown in figure) AB be a ladder and F be the horizontal force to keep it from slipping.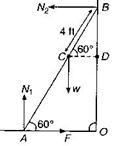
w is the weight of man. Suppose \[{{N}_{1}}\] and \[{{N}_{2}}\] be normal reactions of ground and wall respectively. In horizontal equilibrium, \[{{N}_{2}}F\] In vertical equilibrium, \[{{N}_{1}}=w\] Taking moments about A; Clockwise torque = Anticlockwise torque \[{{N}_{1}}\times CD={{N}_{2}}\times OB\] but in \[\Delta AOB,\,\sin \,\,{{60}^{o}}\,=\frac{OB}{AB}\] \[\Rightarrow OB=AB\sin {{60}^{o}}\] In \[\Delta BCD,\] \[\cos {{60}^{o}}=\frac{CD}{BC}\] \[\Rightarrow CD=BC\,\cos \,{{60}^{o}}\] Substituting in Eq. (i) , we have \[{{N}_{1}}\times BC\,\cos \,\,{{60}^{o}}={{N}_{2}}\times AB\,\sin \,{{60}^{o}}\] \[\Rightarrow w\times BC\times \frac{1}{2}=F\times AB\times \frac{\sqrt{3}}{2}\] Given: w = 150 pound, AB = 20 ft., BC = 4 ft. \[\therefore 150\times 4\times \frac{1}{2}=F\times 20\times \frac{\sqrt{3}}{2}\] \[\Rightarrow F=\frac{150\times 4}{20\sqrt{3}}\] \[=\frac{150\times 4\times \sqrt{3}}{20\times 3}\] = 17.3 pound
You need to login to perform this action.
You will be redirected in
3 sec
