question_answer

                Light enters at an angle of incidence in a transparent rod of refractive index n. For what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidence?                                                        

A)                 \[n>\sqrt{2}\] 

B)                 n = 1

C)                 n = 1.1                  

D)                 n = 1.3

Correct Answer: A

Solution :

                Key Idea: The first idea is that for no refraction at its lateral face, angle of incidence should be greater than critical angle.                 Let a light ray enters at A and refracted beam is AB. At the lateral face, the angle of incidence is \[\theta \]. For no refraction at this face, \[\theta >C\]                 \[\sin \theta >\sin \,C\]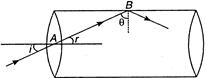                 but  \[\theta +r={{90}^{o}}\] \[\Rightarrow \theta =({{90}^{o}}-r)\] \[\therefore \sin ({{90}^{o}}-r)>\sin \,C\] \[or\cos r>\sin C\]                                           ...(i)                 Key Idea: The second idea is that in Eq. (i), the substitution for cos r can be found from Snell's law. Now from Snell's law.                 Now from Snell?s law,                 \[n=\frac{\sin i}{\sin r}\Rightarrow \sin r=\frac{\sin i}{n}\] \[\therefore \cos r=\sqrt{1-{{\sin }^{2}}r}=\sqrt{\left( 1-\frac{{{\sin }^{2}}i}{{{n}^{2}}} \right)}\] \[\therefore Eq.\,(i)\,gives,\]                 \[\sqrt{1-\frac{{{\sin }^{2}}i}{{{n}^{2}}}}>\sin \,C\]                 \[\Rightarrow 1-\frac{{{\sin }^{2}}i}{{{n}^{2}}}>{{\sin }^{2}}C\]                 Also \[\sin C=\frac{1}{n}\]                 \[\therefore 1-\frac{{{\sin }^{2}}i}{{{n}^{2}}}>\frac{1}{{{n}^{2}}}\] or            \[1>\frac{1}{{{n}^{2}}}+\frac{{{\sin }^{2}}i}{{{n}^{2}}}\] or            \[\frac{1}{{{n}^{2}}}({{\sin }^{2}}i+1)<1\] or            \[{{n}^{2}}>{{\sin }^{2}}i+1\]                 The maximum value of sin i is 1. So, \[\therefore {{n}^{2}}>2\] or            \[n>\sqrt{2}\]