question_answer

                A hollow insulated conducting sphere is given a positive charge of \[10\,\mu C\]. What will be the electric field at the centre of the sphere if its radius is 2 m ?                                                                                  

A)                 Zero   

B)                 \[5\,\mu \,C{{m}^{-2}}\]                              

C)                 \[20\,\mu \,C{{m}^{-2}}\]                           

D)                 \[8\,\mu \,C{{m}^{-2}}\]

Correct Answer: A

Solution :

                     Key Idea: No charge is enclosed by the hollow insulated conducting sphere.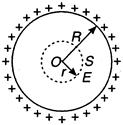                                 Charge resides on the outer surface of a conducting hollow sphere of radius R (say). We consider a spherical surface of radius r < R. By Gauss theorem                 \[\int\limits_{s}^{{}}{\vec{E}\,.\,\overrightarrow{ds}}=\frac{1}{{{\varepsilon }_{0}}}\times \]charge enclosed or            \[E.4\pi {{r}^{2}}=\frac{1}{{{\varepsilon }_{0}}}\times 0\] \[\Rightarrow E=0\]                 i.e., electric field inside a hollow sphere is zero.