A) 3 : 1
B) 1 : 3
C) 1 : 2
D) 2 : 1
Correct Answer: A
Solution :
Key Idea : In a lift weight is the net force acting on the mass while going upwards or downwards. (i) When mass is lifted upwards with an acceleration a, then apparent weight.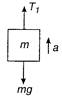 \[{{T}_{1}}-mg=ma\] \[\Rightarrow {{T}_{1}}=mg+ma\] \[{{T}_{1}}=m(g+a)\] Substituting the values, we obtain \[\therefore {{T}_{1}}=(1)\,(9.8+4.9)=14.7\,V\] (ii) When mass is lowered downwards with an acceleration a, then
\[{{T}_{1}}-mg=ma\] \[\Rightarrow {{T}_{1}}=mg+ma\] \[{{T}_{1}}=m(g+a)\] Substituting the values, we obtain \[\therefore {{T}_{1}}=(1)\,(9.8+4.9)=14.7\,V\] (ii) When mass is lowered downwards with an acceleration a, then 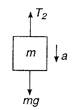 \[mg-{{T}_{2}}=ma\] \[\Rightarrow \,\,{{T}_{2}}=mg-ma=m(g-a)\] Substituting the values, we have \[{{T}_{2}}=(1)\,(9.8-4.9)\,=4.9\,N\] Then, ratio of tensions \[\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{14.7}{4.9}=\frac{3}{1}\] \[\Rightarrow \] \[{{T}_{1}}:{{T}_{2}}=3:1\]
\[mg-{{T}_{2}}=ma\] \[\Rightarrow \,\,{{T}_{2}}=mg-ma=m(g-a)\] Substituting the values, we have \[{{T}_{2}}=(1)\,(9.8-4.9)\,=4.9\,N\] Then, ratio of tensions \[\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{14.7}{4.9}=\frac{3}{1}\] \[\Rightarrow \] \[{{T}_{1}}:{{T}_{2}}=3:1\]
You need to login to perform this action.
You will be redirected in
3 sec
