A) 0.25 A
B) 0.8 A
C) 0.2 A
D) 0.5 A
Correct Answer: B
Solution :
Key Idea: Potential difference across galvanometer should be equal to potential difference across shunt. The shunt and galvanometer are connected as shown in figure. Let the total current through the parallel combination is i, the current through the galvanometer is \[{{i}_{g}}\] and the current through the shunt is \[i-{{i}_{g}}\]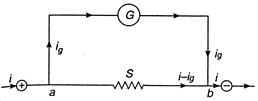 The potential difference \[{{V}_{ab}}\,\,(={{V}_{a}}-{{V}_{b}})\] is the same for both paths, so \[{{i}_{g}}G=(i-{{i}_{g}})S\] \[or{{i}_{g}}(G+S)=i\,S\] \[or\frac{{{i}_{g}}}{i}=\frac{S}{S+G}\] The fraction of current passing through shunt \[=\frac{i-{{i}_{g}}}{i}=1-\frac{{{i}_{g}}}{i}\] \[=1-\frac{S}{S+G}\] \[=\frac{G}{S+G}\] \[=\frac{8}{2+8}\] \[=\frac{8}{10}=0.8\,A\]
The potential difference \[{{V}_{ab}}\,\,(={{V}_{a}}-{{V}_{b}})\] is the same for both paths, so \[{{i}_{g}}G=(i-{{i}_{g}})S\] \[or{{i}_{g}}(G+S)=i\,S\] \[or\frac{{{i}_{g}}}{i}=\frac{S}{S+G}\] The fraction of current passing through shunt \[=\frac{i-{{i}_{g}}}{i}=1-\frac{{{i}_{g}}}{i}\] \[=1-\frac{S}{S+G}\] \[=\frac{G}{S+G}\] \[=\frac{8}{2+8}\] \[=\frac{8}{10}=0.8\,A\]
You need to login to perform this action.
You will be redirected in
3 sec
