A) 1 : 16
B) 4 : 1
C) 1 : 4
D) 1 : 1
Correct Answer: C
Solution :
Key-Idea: Total no. of nuclei remained after n half ?lives is \[N={{N}_{0}}{{\left( \frac{1}{2} \right)}^{n}}\] Total time given = 80 min Number of half-lives of \[A,\,{{n}_{A}}=\frac{80\,\min }{20\,\min }=4\] Number of half-lives of \[B,\,{{n}_{B}}=\frac{80\,\min }{40\,\min }=2\] Number of nuclei remained undecayed \[N={{N}_{0}}{{\left( \frac{1}{2} \right)}^{n}}\] where \[{{N}_{0}}\] is initial number of nuclei \[\therefore \frac{{{N}_{A}}}{{{N}_{B}}}=\frac{{{\left( \frac{1}{2} \right)}^{{{n}_{A}}}}}{{{\left( \frac{1}{2} \right)}^{{{n}_{B}}}}}\] or \[\frac{{{N}_{A}}}{{{N}_{B}}}=\frac{{{\left( \frac{1}{2} \right)}^{4}}}{{{\left( \frac{1}{2} \right)}^{2}}}=\frac{\left( \frac{1}{16} \right)}{\left( \frac{1}{4} \right)}\] or \[\frac{{{N}_{A}}}{{{N}_{B}}}=\frac{1}{4}\] Note: The graph between number of nuclei decayed with time is shown along side.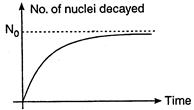
You need to login to perform this action.
You will be redirected in
3 sec
