question_answer

A particle is executing two different simple harmonic motions, mutually perpendicular of different amplitudes and having phase difference of \[\frac{\pi }{2}\]. The path of the particle will be :      [BHU M-2003]

A)  Circular                                               

B)  Straight line      

C)  Parabolic                            

D)  Elliptical

Correct Answer: D

Solution :

                 Let two perpendicular simple harmonic motions are                                                 \[x=A\,\sin \left( \omega t \right)\]                          ?(1)                                                 \[y=B\,\sin \left( \omega t+\phi  \right)\]               ?(2) From Eq. (1) \[\sin \,\left( \omega t \right)=\frac{x}{A}\]                 \[\Rightarrow \]               \[\cos \,\omega t=\sqrt{1-\frac{{{x}^{2}}}{{{A}^{2}}}}\] From Eq. (2)\[\frac{y}{B}=\sin \left( \omega t \right)\cos \phi +\cos \left( \omega t \right)\,\sin \,\phi \] \[=\left( \frac{x}{A} \right)\cos \,\,\phi +\sqrt{1-\frac{{{x}^{2}}}{{{A}^{2}}}}\sin \,\,\phi \]                 \[\Rightarrow \]               \[\frac{y}{B}-\frac{x}{A}\cos \,\,\phi =\sqrt{1-\frac{{{x}^{2}}}{{{A}^{2}}}}\sin \,\,\phi \] On squaring, we get                 \[=\frac{{{y}^{2}}}{{{B}^{2}}}+\frac{{{x}^{2}}}{{{A}^{2}}}{{\cos }^{2}}\,\,\phi -\frac{2xy}{AB}\cos \,\,\phi =\left( 1-\frac{{{x}^{2}}}{{{A}^{2}}} \right){{\sin }^{2}}\,\,\phi \] \[\Rightarrow \frac{{{y}^{2}}}{{{B}^{2}}}+\frac{{{x}^{2}}}{{{A}^{2}}}\left( {{\cos }^{2}}\,\phi +{{\sin }^{2}}\,\,\phi  \right)-\frac{2xy}{AB}\cos \,\,\phi ={{\sin }^{2}}\,\phi \]\[\Rightarrow \frac{{{x}^{2}}}{{{A}^{2}}}+\frac{{{y}^{2}}}{{{B}^{2}}}-\frac{2xy}{AB}\cos \,\phi ={{\sin }^{2}}\,\phi \]       ?(3) When, \[\phi =\frac{\pi }{2},\,\,\cos \,\phi =0,\,\sin \,\phi =1\] Hence, Eq. (3) reduces to                                 \[\frac{{{x}^{2}}}{{{A}^{2}}}+\frac{{{y}^{2}}}{{{B}^{2}}}=1\]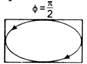 This presents the equation of symmetrical ellipse.