-
question_answer1) Let \[f:R\to R\]be defined by \[f(x)=\frac{\left| x \right|-1}{\left| x \right|+1}\]then f is:
JEE Main Online Paper (Held On 19 April 2016)
A)
both one-one and onto
done
clear
B)
one-one but not onto
done
clear
C)
onto but not one-one
done
clear
D)
neither one-one nor onto.
done
clear
View Answer play_arrow
-
question_answer2) For all complex numbers z of the form \[1+i\alpha ,\alpha \in R,\]if \[{{z}^{2}}=x+iy,\]then
JEE Main Online Paper (Held On 19 April 2016)
A)
\[{{y}^{2}}-4x+2=0\]
done
clear
B)
\[{{y}^{2}}+4x-4=0\]
done
clear
C)
\[{{y}^{2}}-4x-4=0\]
done
clear
D)
\[{{y}^{2}}+4x+2=0\]
done
clear
View Answer play_arrow
-
question_answer3) The equation \[\sqrt{3{{x}^{2}}+x+5}x-3,\]where x is real, has;
JEE Main Online Paper (Held On 19 April 2016)
A)
no solution
done
clear
B)
exactly one solution
done
clear
C)
exactly two solution
done
clear
D)
exactly four solution
done
clear
View Answer play_arrow
-
question_answer4) Let A and B be any two 3 × 3 matrices. If A is symmetric and B is skewsymmetric, then the matrix AB - BA is:
JEE Main Online Paper (Held On 19 April 2016)
A)
skewsymmetric
done
clear
B)
Symmetric
done
clear
C)
neither symmetric nor skewsymmetric
done
clear
D)
I or - I, where I is an identity matrix.
done
clear
View Answer play_arrow
-
question_answer5) If \[\Delta r=\left| \begin{matrix} r & 2r-1 & 3r-2 \\ \frac{n}{2} & n-1 & a \\ \frac{1}{2}n(n-1) & {{(n-1)}^{2}} & \frac{1}{2}(n-1)(3n-4) \\ \end{matrix} \right|\]then the value of\[\sum\limits_{r=1}^{n-1}{{{\Delta }_{r}}}\]
JEE Main Online Paper (Held On 19 April 2016)
A)
depends only on a
done
clear
B)
depends only on n
done
clear
C)
depends both on a and n
done
clear
D)
is independent of both a and n
done
clear
View Answer play_arrow
-
question_answer6) Two women and some men participated in a chess tournament in which every participant played two games with each of the other participants. If the number of games that the men played between themselves exceeds the number of games that the men played with the women by 66, then the number of men who participated in the tournament lies in the interval:
JEE Main Online Paper (Held On 19 April 2016)
A)
[8, 9]
done
clear
B)
[10, 12)
done
clear
C)
(11, 13]
done
clear
D)
(14, 17)
done
clear
View Answer play_arrow
-
question_answer7) The coefficient of \[{{x}^{1012}}\]in the expansion of \[{{(1+{{x}^{n}}+{{x}^{253}})}^{10}},\] (where \[n\le 22\]is any positive integer), is
JEE Main Online Paper (Held On 19 April 2016)
A)
1
done
clear
B)
\[^{10}{{C}_{4}}\]
done
clear
C)
4n
done
clear
D)
\[^{253}{{C}_{4}}\]
done
clear
View Answer play_arrow
-
question_answer8) The number of terms in an A.P. is even; the sum of the odd terms in it is 24 and that the even terms is 30. If the last term exceeds the first term by \[10\frac{1}{2},\] then the number of terms in the A.P. is:
JEE Main Online Paper (Held On 19 April 2016)
A)
4
done
clear
B)
8
done
clear
C)
12
done
clear
D)
16
done
clear
View Answer play_arrow
-
question_answer9) Let \[f(n)=\left[ \frac{1}{3}+\frac{3n}{100} \right]n,\] where [n] denotes the greatest integer less than or equal to n. Then \[\sum\limits_{n=1}^{56}{f\left( n \right)}\]is equal to:
JEE Main Online Paper (Held On 19 April 2016)
A)
56
done
clear
B)
689
done
clear
C)
1287
done
clear
D)
1399
done
clear
View Answer play_arrow
-
question_answer10) If the function\[f\left( x \right)=\left\{ \begin{matrix} \frac{\sqrt{2+\cos x}-1}{{{\left( \pi -x \right)}^{2}}}, & x\ne \pi \\ k & ,x=\pi \\ \end{matrix} \right.\]is continuous at \[x=\pi ,\] then k equals:
JEE Main Online Paper (Held On 19 April 2016)
A)
0
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
2
done
clear
D)
\[\frac{1}{4}\]
done
clear
View Answer play_arrow
-
question_answer11) Let \[f:R\to R\]be a function such that \[\left| f\left( x \right) \right|\le {{x}^{2}},\]for all \[x\in R.\]Then, at x = 0, f is:
JEE Main Online Paper (Held On 19 April 2016)
A)
continuous but not differentiable.
done
clear
B)
continuous as well as differentiable.
done
clear
C)
neither continuous nor differentiable.
done
clear
D)
differentiable but not continuous.
done
clear
View Answer play_arrow
-
question_answer12) If non-zero real numbers b and c are such that min \[f(x)>\max g(x)\] where \[f(x)={{x}^{2}}+2bx+2{{c}^{2}}\]and \[g(x)=-{{x}^{2}}-2cx+{{b}^{2}}\]\[(x\in R);\] then\[\left| \frac{c}{b} \right|\]lies in the interval:
JEE Main Online Paper (Held On 19 April 2016)
A)
\[\left( 0,\frac{1}{2} \right)\]
done
clear
B)
\[\left[ \frac{1}{2},\frac{1}{\sqrt{2}} \right)\]
done
clear
C)
\[\left[ \frac{1}{\sqrt{2},}\sqrt{2} \right]\]
done
clear
D)
\[\left( \sqrt{2},\infty \right)\]
done
clear
View Answer play_arrow
-
question_answer13) If the volume of a spherical ball is increasing at the rate of \[4\pi cc/\sec ,\]then the rate of increase of its radius (in cm/sec), when the volume is \[288\pi cc,\]
JEE Main Online Paper (Held On 19 April 2016)
A)
\[\frac{1}{6}\]
done
clear
B)
\[\frac{1}{9}\]
done
clear
C)
\[\frac{1}{36}\]
done
clear
D)
\[\frac{1}{24}\]
done
clear
View Answer play_arrow
-
question_answer14) If m is a non-zero number and \[\int_{{}}^{{}}{\frac{{{x}^{5m-1}}+2{{x}^{4m-1}}}{{{\left( {{x}^{2m}}+{{x}^{m}}+1 \right)}^{3}}}}dx=f(x)+c,\]then f(x) is:
JEE Main Online Paper (Held On 19 April 2016)
A)
\[\frac{{{x}^{5m}}}{2m{{\left( {{x}^{2m}}+{{x}^{m}}+1 \right)}^{2}}}\]
done
clear
B)
\[\frac{{{x}^{4m}}}{2m{{\left( {{x}^{2m}}+{{x}^{m}}+1 \right)}^{2}}}\]
done
clear
C)
\[\frac{2m\left( {{x}^{5m}}+{{x}^{4m}} \right)}{{{\left( {{x}^{2m}}+{{x}^{m}}+1 \right)}^{2}}}\]
done
clear
D)
\[\frac{\left( {{x}^{5m}}-{{x}^{4m}} \right)}{2m{{\left( {{x}^{2m}}+{{x}^{m}}+1 \right)}^{2}}}\]
done
clear
View Answer play_arrow
-
question_answer15) Let function F be defined as\[F(x)=\int\limits_{1}^{x}{\frac{{{e}^{t}}}{t}}dt,x>0\]then the value of the integral\[\int\limits_{1}^{x}{\frac{{{e}^{t}}}{t+a}}dt,\]where a > 0, is:
JEE Main Online Paper (Held On 19 April 2016)
A)
\[{{e}^{a}}\left[ F(x)-F(1+a) \right]\]
done
clear
B)
\[{{e}^{-a}}\left[ F(x+a)-F(a) \right]\]
done
clear
C)
\[{{e}^{a}}\left[ F(x+a)-F(1+a) \right]\]
done
clear
D)
\[{{e}^{-a}}\left[ F(x+a)-F(1+a) \right]\]
done
clear
View Answer play_arrow
-
question_answer16) The area of the region above the x-axis bounded by the curve \[y=\tan x,0\le x\le \frac{\pi }{2}\]and the tangent to the curve at \[x=\frac{\pi }{4}\] is:
JEE Main Online Paper (Held On 19 April 2016)
A)
\[\frac{1}{2}\left( \log 2-\frac{1}{2} \right)\]
done
clear
B)
\[\frac{1}{2}\left( \log 2+\frac{1}{2} \right)\]
done
clear
C)
\[\frac{1}{2}\left( 1-\log 2 \right)\]
done
clear
D)
\[\frac{1}{2}\left( 1+\log 2 \right)\]
done
clear
View Answer play_arrow
-
question_answer17) If\[\frac{dy}{dx}+y\tan x=\sin 2x\]and\[y(0)=1,\]then\[y(\pi )\] then y(p) is equal to:
JEE Main Online Paper (Held On 19 April 2016)
A)
1
done
clear
B)
-1
done
clear
C)
-5
done
clear
D)
5
done
clear
View Answer play_arrow
-
question_answer18) The circumcentre of a triangle lies at the origin and its centroid is the mid point of the line segment joining the points \[({{a}^{2}}+1,{{a}^{2}}+1)\]and \[(2a,-2a),a\ne 0.\]Then for any a, the orthocentre of this triangle lies on the line:
JEE Main Online Paper (Held On 19 April 2016)
A)
\[y-2ax=0\]
done
clear
B)
\[y-({{a}^{2}}+1)x=0\]
done
clear
C)
\[y+x=0\]
done
clear
D)
\[{{(a-1)}^{2}}x-{{(a+1)}^{2}}y=0\]
done
clear
View Answer play_arrow
-
question_answer19) If a line L is perpendicular to the line \[5x-y=1\], and the area of the triangle formed by the line L and the coordinate axes is 5, then the distance of line L from the line \[x+5y=0\] is:
JEE Main Online Paper (Held On 19 April 2016)
A)
\[\frac{7}{\sqrt{5}}\]
done
clear
B)
\[\frac{5}{\sqrt{13}}\]
done
clear
C)
\[\frac{7}{\sqrt{13}}\]
done
clear
D)
\[\frac{5}{\sqrt{7}}\]
done
clear
View Answer play_arrow
-
question_answer20) The equation of circle described on the chord \[3x+y+5=0\]of the circle \[{{x}^{2}}+{{y}^{2}}=16\]as diameter is:
JEE Main Online Paper (Held On 19 April 2016)
A)
\[{{x}^{2}}+{{y}^{2}}+3x+y-11=0\]
done
clear
B)
\[{{x}^{2}}+{{y}^{2}}+3x+y+1=0\]
done
clear
C)
\[{{x}^{2}}+{{y}^{2}}+3x+y-2=0\]
done
clear
D)
\[{{x}^{2}}+{{y}^{2}}+3x+y-22=0\]
done
clear
View Answer play_arrow
-
question_answer21) A chord is drawn through the focus of the parabola \[{{y}^{2}}=6x\]such that its distance from the vertex of this parabola is \[\frac{\sqrt{5}}{2},\]then its slope can be:
JEE Main Online Paper (Held On 19 April 2016)
A)
\[\frac{\sqrt{5}}{2}\]
done
clear
B)
\[\frac{\sqrt{3}}{2}\]
done
clear
C)
\[\frac{2}{\sqrt{5}}\]
done
clear
D)
\[\frac{2}{\sqrt{3}}\]
done
clear
View Answer play_arrow
-
question_answer22) The tangent at an extremity (in the first quadrant) of latus rectum of the hyperbola \[\frac{{{x}^{2}}}{4}-\frac{{{y}^{2}}}{5}=1,\] meet x-axis and y-axis at A and B respectively. Then \[{{(OA)}^{2}}-{{(OB)}^{2}},\]where O is the origin, equals:
JEE Main Online Paper (Held On 19 April 2016)
A)
\[-\frac{20}{9}\]
done
clear
B)
\[\frac{19}{9}\]
done
clear
C)
4
done
clear
D)
\[-\frac{4}{3}\]
done
clear
View Answer play_arrow
-
question_answer23) Equation of the line of the shortest distance between the lines \[\frac{x}{1}=\frac{y}{-1}=\frac{z}{1}\]and \[\frac{x-1}{0}=\frac{y+1}{-2}=\frac{z}{1}\]is:
JEE Main Online Paper (Held On 19 April 2016)
A)
\[\frac{x}{1}=\frac{y}{-1}=\frac{z}{-2}\]
done
clear
B)
\[\frac{x-1}{1}=\frac{y+1}{-1}=\frac{z}{-2}\]
done
clear
C)
\[\frac{x-1}{1}=\frac{y+1}{-1}=\frac{z}{1}\]
done
clear
D)
\[\frac{x}{-2}=\frac{y}{1}=\frac{z}{2}\]
done
clear
View Answer play_arrow
-
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
-
A)
12
done
clear
B)
15
done
clear
C)
14
done
clear
D)
13
done
clear
View Answer play_arrow
-
question_answer26)
Let A and E be any two events with positive probabilities: Statement - 1:  Statement ? 2:
Statement ? 2:  JEE Main Online Paper (Held On 19 April 2016)
JEE Main Online Paper (Held On 19 April 2016)
A)
Both the statements are true
done
clear
B)
Both the statements are false
done
clear
C)
Statement-1 is true, Statement-2 is false
done
clear
D)
Statement-1 is false, Statement-2 is true
done
clear
View Answer play_arrow
-
A)
Statement I and Statement II are both false
done
clear
B)
Statement I and Statement II are both true
done
clear
C)
Statement I is true and Statement II is false
done
clear
D)
Statement I is false and Statement II is true
done
clear
View Answer play_arrow
-
question_answer28)
The function 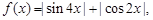 is a periodic function with period:
JEE Main Online Paper (Held On 19 April 2016)
is a periodic function with period:
JEE Main Online Paper (Held On 19 April 2016)
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
-
question_answer29)
The principal value of 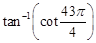 is:
JEE Main Online Paper (Held On 19 April 2016)
is:
JEE Main Online Paper (Held On 19 April 2016)
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Answer play_arrow
-
question_answer30) The contrapositive of the statement 'if I am not feeling well, then I will go to the doctor' is
JEE Main Online Paper (Held On 19 April 2016)
A)
If I am feeling well, then I will not go to the doctor
done
clear
B)
If I will go to the doctor, then I am feeling well
done
clear
C)
If I will not go to the doctor, then I am feeling well
done
clear
D)
If I will go to the doctor, then I am not feeling well.
done
clear
View Answer play_arrow
