-
question_answer1) Given a sequence of 4 numbers, first three of with are in G.P. and the last there are in A.P. with common difference six If first and last terms of this sequence are equal then the last term is :
JEE Main Online Paper ( Held On 25 April 2013 )
A)
16
done
clear
B)
8
done
clear
C)
4
done
clear
D)
2
done
clear
View Answer play_arrow
-
question_answer2)
Statement I: The only circle having radius\[\sqrt{10}\] and a diameter along line 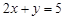 is \[{{x}^{2}}+{{y}^{2}}-6x+2y=0.\] Statement II:\[2x+y=5\] is a normal to the circle \[{{x}^{2}}+{{y}^{2}}-6x-2y=0.\]
JEE Main Online Paper ( Held On 25 April 2013 )
is \[{{x}^{2}}+{{y}^{2}}-6x+2y=0.\] Statement II:\[2x+y=5\] is a normal to the circle \[{{x}^{2}}+{{y}^{2}}-6x-2y=0.\]
JEE Main Online Paper ( Held On 25 April 2013 )
A)
Statement I is false; statement II is true.
done
clear
B)
Statement I is true; Statement II is true; Statement II is a correct explanation for Statement I.
done
clear
C)
Statement I is true; Statement II is false.
done
clear
D)
Statement I is true; Statement II is true; Statement II is not a correct explanation for Statement I.
done
clear
View Answer play_arrow
-
question_answer3) If a circle of unit radius is divided into two parts by an arc of another circle subtending an angle \[{{60}^{o}}\]on the circumference of the first circle, then the of the first circle, then the radius of the are is:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[\sqrt{3}\]
done
clear
B)
\[\frac{1}{2}\]
done
clear
C)
\[1\]
done
clear
D)
\[\sqrt{2}\]
done
clear
View Answer play_arrow
-
question_answer4) If the image of point P(2,3) in a line L is Q(4,5), the image of point R(0,0) in the same line is :
JEE Main Online Paper ( Held On 25 April 2013 )
A)
(2, 2)
done
clear
B)
(4, 5)
done
clear
C)
(3, 4)
done
clear
D)
(7, 7)
done
clear
View Answer play_arrow
-
question_answer5) Consider the system of equations: \[x+ay=0,\]\[y+az=0\]and\[z+ax=0\]. Then the set of all real values of ?a? for with the system has a unique solution is:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[R-\{1\}\]
done
clear
B)
\[R-\{-1\}\]
done
clear
C)
\[\{1,-1\}\]
done
clear
D)
\[\{1,0,-1\}\]
done
clear
View Answer play_arrow
-
question_answer6)
A common tangent to the conics 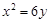 and \[2{{x}^{2}}-4{{y}^{2}}=9\]is :
JEE Main Online Paper ( Held On 25 April 2013 )
and \[2{{x}^{2}}-4{{y}^{2}}=9\]is :
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[x-y=\frac{3}{2}\]
done
clear
B)
\[x+y=1\]
done
clear
C)
\[x+y=\frac{9}{2}\]
done
clear
D)
\[x-y=1\]
done
clear
View Answer play_arrow
-
question_answer7) Let \[\operatorname{S}=\left\{ \left( \begin{matrix} {{a}_{11}} & {{a}_{12}} \\ {{a}_{21}} & {{a}_{22}} \\ \end{matrix} \right):{{a}_{\operatorname{i}\operatorname{j}}}\in \{0,1,2\},{{a}_{11}}={{a}_{22}} \right\}\] Then the number of non ? singular matrices in the set S is:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
27
done
clear
B)
24
done
clear
C)
10
done
clear
D)
20
done
clear
View Answer play_arrow
-
question_answer8) Let \[x\]\[\in \](0, 1). The set of all \[x\] such that\[\text{si}{{\text{n}}^{-\text{1}}}x>{{\cos }^{-1}}x,\] is the interval :
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[\left( \frac{1}{2},\frac{1}{\sqrt{2}} \right)\]
done
clear
B)
\[\left( \frac{1}{\sqrt{2}},1 \right)\]
done
clear
C)
\[\left( 0,1 \right)\]
done
clear
D)
\[\left( 0,\frac{\sqrt{3}}{2} \right)\]
done
clear
View Answer play_arrow
-
question_answer9) Let A (-3,2) and B(-2,1) be the vertices of a triangle ABC. If the centroid of this triangle lies on the line \[3x+4y+2=0,\] the vertex C lies on the line:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[4x+3y+5=0\]
done
clear
B)
\[3x+4y+3=0\]
done
clear
C)
\[4x+3y+3=0\]
done
clear
D)
\[3x+4y+5=0\]
done
clear
View Answer play_arrow
-
question_answer10) Let ABC be a triangle with vertices at points A (2,3,5), B (-1,3,2) and C (\[\lambda ,5,\mu \]) in three dimensional space. If the median through A is equally inclined with the axes, the is\[\left( \lambda ,\mu \right)\]equal to:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[\left( 10,7 \right)\]
done
clear
B)
\[\left( 7,5 \right)\]
done
clear
C)
\[\left( 7,10 \right)\]
done
clear
D)
\[\left( 5,7 \right)\]
done
clear
View Answer play_arrow
-
question_answer11) If the integral \[\int{\frac{\cos 8x+1}{\cot 2x-\tan 2x}dx=A\cos }\]\[8x+k,\]where K is an arbitrary constant, then A is equal to :
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[-\frac{1}{16}\]
done
clear
B)
\[\frac{1}{16}\]
done
clear
C)
\[\frac{1}{8}\]
done
clear
D)
\[-\frac{1}{8}\]
done
clear
View Answer play_arrow
-
question_answer12) The equation of the curve passing through the origin and satisfying the differential equation \[(1+{{x}^{2}})\frac{\operatorname{dy}}{\operatorname{dx}}+2xy=4{{x}^{2}}\]is :
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[(1+{{x}^{2}})y={{x}^{3}}\]
done
clear
B)
\[3(1+{{x}^{2}})y=2{{x}^{3}}\]
done
clear
C)
\[1(1+{{x}^{2}})y=3{{x}^{3}}\]
done
clear
D)
\[3(1+{{x}^{2}})y=4{{x}^{3}}\]
done
clear
View Answer play_arrow
-
question_answer13) For\[0\le x\le \frac{\pi }{2},\] the value of\[\int\limits_{0}^{{{\sin }^{2}}x}{{{\sin }^{-1}}(\sqrt{t})\operatorname{dt}+}\int\limits_{0}^{{{\cos }^{2}}x}{{{\cos }^{-1}}(\sqrt{t})\operatorname{dt}}\]equals:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[\frac{\pi }{4}\]
done
clear
B)
0
done
clear
C)
1
done
clear
D)
\[-\frac{\pi }{4}\]
done
clear
View Answer play_arrow
-
question_answer14) Let f: \[\left[ -2,3 \right]\to \left[ 8,\infty \right]\]be a continuous function such that \[f(1-x)=f(x)\] for all \[x\in [-1,3].\] If \[{{\operatorname{R}}_{1}}\]is the numerical value of the area of the region bounded by \[y=f(x),x=-2\], \[x=3\]and the axis of \[x\] and\[{{R}_{2}}=\int\limits_{-2}^{3}{xf(x)\operatorname{d}x,\operatorname{then}:}\]
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[3{{R}_{1}}=2{{R}_{2}}\]
done
clear
B)
\[2{{R}_{1}}=3{{R}_{2}}\]
done
clear
C)
\[{{R}_{1}}={{R}_{2}}\]
done
clear
D)
\[{{R}_{1}}=2{{R}_{2}}\]
done
clear
View Answer play_arrow
-
question_answer15) Let\[\vec{a}=2\hat{i}+\hat{j}-2\hat{k},\,\vec{b}=\hat{i}+\hat{j}\]. If\[\vec{c}\] is a vector such that \[\vec{a}\cdot \vec{c}=|\vec{c}|,\,|\vec{c}-\vec{a}|=2\sqrt{2}\]and the angle between \[\vec{a}\times \vec{b}\] and \[\vec{c}\]is \[{{30}^{o}}\], then \[|(\vec{a}\times \vec{b})\times \vec{c}|\] equals:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[\frac{1}{2}\]
done
clear
B)
\[\frac{3\sqrt{3}}{2}\]
done
clear
C)
3
done
clear
D)
\[\frac{3}{2}\]
done
clear
View Answer play_arrow
-
question_answer16) Let p and q be any two logical statements and \[\operatorname{r}:p\to (\sim \operatorname{p}\vee \operatorname{q}).\]If r has truth values of p and q are respectively:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
F, F
done
clear
B)
T, T
done
clear
C)
T, F
done
clear
D)
F, T
done
clear
View Answer play_arrow
-
question_answer17) If the events A and B are mutually exclusive events such that \[\operatorname{P}(\operatorname{A})=\frac{3x+1}{3}\]\[\operatorname{P}(\operatorname{B})=\frac{1+x}{4},\] then the set of possible values of \[x\] lies in the interval:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[\left[ 0,1 \right]\]
done
clear
B)
\[\left[ \frac{1}{3},\frac{1}{3} \right]\]
done
clear
C)
\[\left[ -\frac{1}{3},\frac{5}{9} \right]\]
done
clear
D)
\[\left[ -\frac{7}{9},\frac{4}{9} \right]\]
done
clear
View Answer play_arrow
-
question_answer18) The equation of a plane though the of intersection of the planes \[x+2y=3,\]of the planes \[x+2y=3,\]\[y-2z+1=0\] and perpendicular to the first plane is:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[2x-y-10z=9\]
done
clear
B)
\[2x-y+7z=11\]
done
clear
C)
\[2x-y+10z=11\]
done
clear
D)
\[2x-y-9z=10\]
done
clear
View Answer play_arrow
-
question_answer19) If for positive integers\[\operatorname{r}>1,\operatorname{n},>2,\]the coefficients of the \[{{(3r)}^{\operatorname{th}}}\]and \[{{(\operatorname{r}+2)}^{\operatorname{th}}}\] powers of \[x\]in the expansion of \[{{(1+x)}^{2n}}\] are equal, then n is equal to
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[2r+1\]
done
clear
B)
\[2r-1\]
done
clear
C)
3r
done
clear
D)
\[r+1\]
done
clear
View Answer play_arrow
-
question_answer20) If p and q are non-zero real numbers and\[{{\alpha }^{3}}+{{\beta }^{3}}=-p,\,\,\alpha \beta =q,\]then a quadratic equation whose roots are\[\frac{{{\alpha }^{2}}}{\beta },\frac{{{\beta }^{2}}}{\alpha }\]is:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[p{{x}^{2}}-qx+{{p}^{2}}=0\]
done
clear
B)
\[q{{x}^{2}}+px+{{q}^{2}}=0\]
done
clear
C)
\[p{{x}^{2}}+qx+{{p}^{2}}=0\]
done
clear
D)
\[q{{x}^{2}}-px+{{q}^{2}}=0\]
done
clear
View Answer play_arrow
-
question_answer21) A spherical balloon is being inflated at the rate of 35cc/min. The rate of increase in the surface area (in\[{{\operatorname{cm}}^{2}}/\min .\]) of the balloon when its diameter is 14 cm, is
JEE Main Online Paper ( Held On 25 April 2013 )
A)
10
done
clear
B)
\[\sqrt{10}\]
done
clear
C)
\[100\]
done
clear
D)
\[10\sqrt{10}\]
done
clear
View Answer play_arrow
-
question_answer22) Let \[\operatorname{A}=\{\theta :\sin (\theta )=\tan (\theta )\}\] and \[B=\{\theta :\cos (\theta )=1\}\] be two sets. Then:
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[\operatorname{A}=B\]
done
clear
B)
\[\operatorname{A}\not\subset B\]
done
clear
C)
\[\operatorname{B}\not\subset \operatorname{A}\]
done
clear
D)
\[A\subset B\]and\[B-A\ne \phi \]
done
clear
View Answer play_arrow
-
question_answer23) Let z satisfy \[\left| z \right|=1\] and \[\left| z \right|=1-\overset{-}{\mathop{z}}\,\] Statement I : z is a real number Statement II : Principal argument of\[z\] is \[\frac{\pi }{3}\]
JEE Main Online Paper ( Held On 25 April 2013 )
A)
Statement I true: Statement II is true; Statement II is a correct explanation for statement I
done
clear
B)
Statement I is false; Statement II is true.
done
clear
C)
Statement I is true; statement II is false.
done
clear
D)
Statement I is true; Statement II is true; Statement II is not a correct explanation for Statement I.
done
clear
View Answer play_arrow
-
question_answer24) Consider the function \[f(x)=[x]+\left| 1-x \right|,-1\le x\le 3\]where\[\left[ x \right]\]is the greatest integer function. Statement I: \[f\]in not continuous at \[x=0,\]1,2 and 3. Statement II: \[f(x)\left( \begin{matrix} -x, & -1\le x<0 \\ 1-x, & 0\le x<1 \\ 1+x, & 1\le x<2 \\ 2+x, & 2\le x\le 3 \\ \end{matrix} \right.\]
A)
Statement I is true; Statement II is false.
done
clear
B)
done
clear
C)
Statement I is true: Statement II is true; Statement II is a correct explanation for Statement I.
done
clear
D)
Statement I is false; Statement ii is true.
done
clear
View Answer play_arrow
-
question_answer25) Let \[f(1)=-2\] and \[f'(x)\ge 4.2\] for 1 \[\le x\le 6.\]The possible value of \[f(6)\] lies in the interval
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[\left( 15,19 \right)\]
done
clear
B)
\[\left( -\infty ,12 \right)\]
done
clear
C)
\[[12,\,15)\]
done
clear
D)
\[[19,\,\infty )\]
done
clear
View Answer play_arrow
-
question_answer26) In a set of 2n observations, half of them ear equal to \['a'\] and the remaining half are equal to \['-a'\] If the standard deviation of all the observations is 2; then the value of \[\left| a \right|\]is :
JEE Main Online Paper ( Held On 25 April 2013 )
A)
2
done
clear
B)
\[\sqrt{2}\]
done
clear
C)
4
done
clear
D)
\[2\sqrt{2}\]
done
clear
View Answer play_arrow
-
question_answer27) The value of\[{{1}^{2}}+{{3}^{2}}+{{5}^{2}}+..........+{{25}^{2}}\]is :
JEE Main Online Paper ( Held On 25 April 2013 )
A)
2925
done
clear
B)
1469
done
clear
C)
1728
done
clear
D)
1456
done
clear
View Answer play_arrow
-
question_answer28) If an equation of a tangent to the curve,\[y=\cos (x+y),-1\le x\le 1+\pi \], is \[x+2y=k\]then \[k\]is equal to
JEE Main Online Paper ( Held On 25 April 2013 )
A)
1
done
clear
B)
2
done
clear
C)
\[\frac{\pi }{4}\]
done
clear
D)
\[\frac{\pi }{2}\]
done
clear
View Answer play_arrow
-
question_answer29) 5-digit numbers are to be formed using 2,3,5,7,9 without repeating the digits. If p be the number of such numbers that exceed 20000 and \[q\] be the number of those that lie between 30000 and 90000 , then p:q is :
JEE Main Online Paper ( Held On 25 April 2013 )
A)
6:5
done
clear
B)
3:2
done
clear
C)
4:3
done
clear
D)
5:3
done
clear
View Answer play_arrow
-
question_answer30) A point on the ellipse,\[4{{x}^{2}}+9{{y}^{2}}=36,\]where the normal is parallel to the line, \[4x-2y-5=0,\]is :
JEE Main Online Paper ( Held On 25 April 2013 )
A)
\[\left( \frac{9}{5},\frac{8}{5}, \right)\]
done
clear
B)
\[\left( \frac{8}{5},-\frac{9}{5}, \right)\]
done
clear
C)
\[\left( -\frac{9}{5},\frac{8}{5}, \right)\]
done
clear
D)
\[\left( -\frac{8}{5},\frac{9}{5} \right)\]
done
clear
View Answer play_arrow
