A) \[1\]
B) \[2\]
C) \[4\]
D) None of these
Correct Answer: B
Solution :
Given equation of sphere, \[{{(x-2)}^{2}}+{{(y-2)}^{2}}+{{(z-1)}^{2}}={{r}^{2}}\] Here, centre of sphere \[=(2,2,1)\] Let radius \[=r\] Equation of a plane is, \[2x-2y+z+5=0\]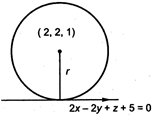 Now, r = perpendicular distance on the plane from the centre of the sphere \[r=\frac{|2(2)-2(2)+(1)+5|}{\sqrt{4+4+1}}=\frac{|4-4+1+5|}{\sqrt{9}}\] \[r=\frac{6}{3}=2\]
Now, r = perpendicular distance on the plane from the centre of the sphere \[r=\frac{|2(2)-2(2)+(1)+5|}{\sqrt{4+4+1}}=\frac{|4-4+1+5|}{\sqrt{9}}\] \[r=\frac{6}{3}=2\]
You need to login to perform this action.
You will be redirected in
3 sec
