question_answer

    A line with direction cosines proportional to 2,1, 2 meets each of the lines\[x=y+a=z\]and \[x+a=2y=2z\]. The co-ordinates of each of the points of intersection are given by

A)  \[(3a,3a,3a)(a,a,a)\]

B)  \[(3a,2a,3a)(a,a,a)\]

C)  \[(3a,2a,3a)(a,a,2a)\]

D)  \[(2a,3a,3a)(2a,a,a)\]

Correct Answer: B

Solution :

                Let the equation of line AB is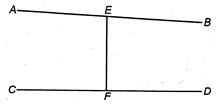 \[\frac{x-0}{1}=\frac{y+a}{1}=\frac{z-0}{1}=k\] (say) \[\therefore \]Co-ordinates off are\[(k,k-a,k)\]. Also the equation of other line CD is \[\frac{x+a}{2}=\frac{y-0}{1}=\frac{z-0}{1}=\lambda \](say) \[\therefore \]Co-ordinates off are\[(2\lambda -a,\lambda ,\lambda )\] Direction Ratio of EF are \[(k-2\lambda +a),\]\[(k-\lambda -a),(k-\lambda )\] \[\therefore \]  \[\frac{k-2\lambda +a}{2}=\frac{k-\lambda -a}{1}=\frac{k-\lambda }{2}\] On solving first and second fraction.                 \[\frac{k-2\lambda +a}{2}=\frac{k-\lambda -a}{1}\] \[\Rightarrow \]               \[k-2\lambda +a=2k-2\lambda -2a\] \[\Rightarrow \]                               \[k=3a\] On solving second and third fraction \[\frac{k-\lambda -a}{1}=\frac{k-\lambda }{2}\] \[\Rightarrow \]               \[2k-2\lambda -2a=k-\lambda \] \[\Rightarrow \]               \[k-\lambda =2a\] \[\Rightarrow \]               \[\lambda =k-2a=3a-2a\] \[\Rightarrow \]               \[\lambda =a\] \[\therefore \]  Co-ordinates of\[E=(3a,\text{ }2a,\text{ }3a)\]and co-ordinates of\[F=(a,a,a)\].