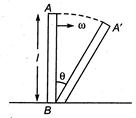
A) \[\sqrt{\frac{6g}{l}}\sin \theta \]
B) \[\sqrt{\frac{6g}{l}}\sin \frac{\theta }{2}\]
C) \[\sqrt{\frac{6g}{l}}\cos \frac{\theta }{2}\]
D) \[\sqrt{\frac{6g}{l}}\cos \theta \]
Correct Answer: B
Solution :
The fall of centre of mass \[h=\frac{l}{2}(1-\cos \theta )\]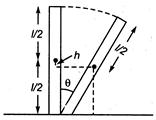 \[\therefore \]Decrease in potential energy\[=mgh\] \[=mg\frac{l}{2}(1-cos\theta )\] From law of conservation of energy, KE\[o\] rotation = decrease in PE \[\frac{1}{2}I{{\omega }^{2}}=\frac{mgl}{2}(1-\cos \theta )\] \[\frac{1}{2}\frac{m{{l}^{2}}}{3}{{\omega }^{2}}=\frac{mgl}{2}(1-\cos \theta )\] \[{{\omega }^{2}}=\frac{6g}{2l}(1-\cos \theta )\] \[=\frac{6g}{2l}2{{\sin }^{2}}\frac{\theta }{2}\] \[\omega =\sqrt{\frac{6g}{l}{{\sin }^{2}}\frac{\theta }{2}}\] \[=\sqrt{\frac{6g}{l}}\sin \frac{\theta }{2}\]
\[\therefore \]Decrease in potential energy\[=mgh\] \[=mg\frac{l}{2}(1-cos\theta )\] From law of conservation of energy, KE\[o\] rotation = decrease in PE \[\frac{1}{2}I{{\omega }^{2}}=\frac{mgl}{2}(1-\cos \theta )\] \[\frac{1}{2}\frac{m{{l}^{2}}}{3}{{\omega }^{2}}=\frac{mgl}{2}(1-\cos \theta )\] \[{{\omega }^{2}}=\frac{6g}{2l}(1-\cos \theta )\] \[=\frac{6g}{2l}2{{\sin }^{2}}\frac{\theta }{2}\] \[\omega =\sqrt{\frac{6g}{l}{{\sin }^{2}}\frac{\theta }{2}}\] \[=\sqrt{\frac{6g}{l}}\sin \frac{\theta }{2}\]
You need to login to perform this action.
You will be redirected in
3 sec
