A) \[1.5\,\,N/C\]
B) \[1.5\times {{10}^{-10}}N/C\]
C) \[3\,\,N/C\]
D) \[3\times {{10}^{-10}}N/C\]
Correct Answer: C
Solution :
The situation is shown in the figure. Plate \[1\] has surface charge density \[\sigma \] and plate \[2\] has surface charge density \[-\sigma \]. The electric field at point \[P\] due to two charged plates add up, giving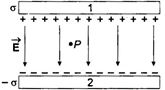 \[E=\frac{\sigma }{2{{\varepsilon }_{0}}}+\frac{\sigma }{2{{\varepsilon }_{0}}}=\frac{\sigma }{{{\varepsilon }_{0}}}\] Given, \[\sigma =26.4\times {{10}^{-12}}C/{{m}^{2}}\] \[{{\varepsilon }_{0}}=8.85\times {{10}^{-12}}C/N\text{-}{{m}^{2}}\] Hence, \[E=\frac{26.4\times {{10}^{-12}}}{8.85\times {{10}^{-12}}}\approx 3\,\,N/C\] Note: The direction of electric field is from the positive to the negative plate.
\[E=\frac{\sigma }{2{{\varepsilon }_{0}}}+\frac{\sigma }{2{{\varepsilon }_{0}}}=\frac{\sigma }{{{\varepsilon }_{0}}}\] Given, \[\sigma =26.4\times {{10}^{-12}}C/{{m}^{2}}\] \[{{\varepsilon }_{0}}=8.85\times {{10}^{-12}}C/N\text{-}{{m}^{2}}\] Hence, \[E=\frac{26.4\times {{10}^{-12}}}{8.85\times {{10}^{-12}}}\approx 3\,\,N/C\] Note: The direction of electric field is from the positive to the negative plate.
You need to login to perform this action.
You will be redirected in
3 sec
