A) \[20\sqrt{\frac{25}{538}}\,V\]and \[\frac{10}{\sqrt{538}}A\]
B) \[10\sqrt{\frac{250}{528}}\,V\]and \[\frac{10}{\sqrt{538}}A\]
C) \[\sqrt{\frac{250}{538}}\,V\]and \[\frac{1}{\sqrt{538}}A\]
D) \[\sqrt{\frac{125}{539}}\,V\]and \[\frac{1}{\sqrt{538}}\,A\]
Correct Answer: B
Solution :
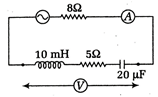
Impedance of the circuit is \[Z=\sqrt{{{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}}\] \[R=8\,\Omega \] (given) \[{{X}_{L}}=\omega L=1000\times 10\times {{10}^{-3}}=10\,\Omega \] \[{{X}_{C}}=\frac{1}{\omega C}=\frac{1}{2000\times 20\times {{10}^{-6}}}=25\,\Omega \] \[\Rightarrow \]\[Z=\sqrt{64+{{(15)}^{2}}}=\sqrt{64+225}=\sqrt{269}\] \[{{I}_{\max }}=\frac{{{V}_{0}}}{Z}=\frac{10}{\sqrt{269}}A\] \[{{I}_{rms}}=\frac{{{\operatorname{I}}_{max}}}{\sqrt{2}}=\frac{10}{\sqrt{538}}A\] \[{{V}_{rms}}={{I}_{rms}}\times \sqrt{{{5}^{2}}+{{(15)}^{2}}}\] \[=\frac{10}{\sqrt{538}}\times \sqrt{25+225}=10\sqrt{\frac{250}{538}}\,V\]You need to login to perform this action.
You will be redirected in
3 sec
