A) \[3<a<10\]
B) \[a\ge 10\]
C) \[-2<a<3\]
D) (d) \[a\le -2\]
Correct Answer: C
Solution :
If one root is less than \[\alpha \] other root is greater than \[\beta \], then \[D\ge 0\] and \[f(\alpha )<0,\,\,f(\beta )<0\] Here, equation is \[{{x}^{2}}-(a+1)\,x+{{a}^{2}}+a-8=0\] \[{{(a+1)}^{2}}-4({{a}^{2}}+a-8)\ge 0\] \[\Rightarrow \] \[{{a}^{2}}+1+2a-4{{a}^{2}}-4a+32\ge 0\] \[\Rightarrow \] \[-3{{a}^{2}}-2a+33\ge 0\] \[\Rightarrow \] \[3{{a}^{2}}+2a+33\ge 0\] \[\Rightarrow \] \[3{{a}^{2}}+11a-9a-33\le 0\] \[\Rightarrow \] \[a(3a+11)-3(3a+11)\le 0\] \[\Rightarrow \] \[(3a+11)\,(a-3)\le 0\]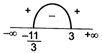 \[\Rightarrow \] \[a\in \,\left[ \frac{-11}{3},\,3 \right]\] \[f(2)<0\] \[4-(a+1)\,.\,2+{{a}^{2}}+a-8<0\] \[4-2a-2+{{a}^{2}}+a-8<0\] \[{{a}^{2}}-a-6<0\]
\[\Rightarrow \] \[a\in \,\left[ \frac{-11}{3},\,3 \right]\] \[f(2)<0\] \[4-(a+1)\,.\,2+{{a}^{2}}+a-8<0\] \[4-2a-2+{{a}^{2}}+a-8<0\] \[{{a}^{2}}-a-6<0\] You need to login to perform this action.
You will be redirected in
3 sec
