question_answer

The minimum area of a triangle formed by any tangent to the ellipse\[\frac{{{x}^{2}}}{16}+\frac{{{y}^{2}}}{81}=1\]and the co-ordinate axes is:   [JEE Main Online Paper ( Held On 12 Apirl  2014 )

A) 12                                          

B) 18

C) 26                                          

D) 36

Correct Answer: D

Solution :

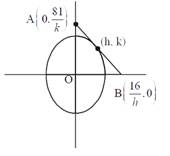                Let (h, k) be the point on ellipse through which tangent is passing. Equation of tangent at \[(h,k)=\frac{xh}{16}+\frac{yk}{81}=1\] at \[y=0,x=\frac{16}{h}\] at\[x=0,y=\frac{81}{k}\] Area of \[AOB=\frac{1}{2}\times \left( \frac{16}{h} \right)\times \left( \frac{81}{k} \right)=\frac{648}{hk}\] \[{{A}^{2}}=\frac{{{(648)}^{2}}}{{{h}^{2}}{{k}^{2}}}\]                                                       ?(1) (h, k) must satisfy equation of ellipse \[=\frac{{{h}^{2}}}{16}+\frac{{{k}^{2}}}{81}=1\] \[{{h}^{2}}=\frac{16}{81}+(81-{{k}^{2}})\] Putting value of \[{{h}^{2}}\]in equation (1) \[{{A}^{2}}=\frac{81{{(648)}^{2}}}{16\times {{k}^{2}}(81-{{k}^{2}})}=\frac{\alpha }{81{{k}^{2}}-{{k}^{4}}}\] differentiating w.r. to k \[2A{{A}^{'}}=\alpha \left( \frac{-1}{81{{k}^{2}}-{{k}^{4}}} \right)=(162k-4{{k}^{3}})\] \[2A{{A}^{'}}=-2A(81k-4{{k}^{3}})\Rightarrow A'=-81k-4{{k}^{3}}\] Put\[A'=0\] \[\Rightarrow \]\[162k-4{{k}^{3}}=0,k(162-4{{k}^{2}})=0\] \[\Rightarrow \]\[k=0,k=\pm \frac{9}{\sqrt{2}}\] \[A''=-(81-12{{k}^{2}})\] For both value of \[k,A''=405>0\] Area will be minimum for \[k=\pm \frac{9}{\sqrt{2}}\] \[{{h}^{2}}=\frac{16}{81}(81-{{k}^{2}})=8\] \[h=\pm 2\sqrt{2}\] Area of triangle \[AOB=\frac{648\times \sqrt{2}}{2\sqrt{2}\times 9}=36\]sq unit