A) 5
B) \[2\sqrt{5}\]
C) 4
D) \[\sqrt{57}\]
Correct Answer: A
Solution :
Let A be the centre of given circle and B be the centre of circle C.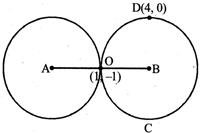 \[{{x}^{2}}+{{y}^{2}}+4x-6y-12=0\] \[\therefore \] \[A=(-2,3)\]and \[B=(g,f)\] Now, from the figure, we have \[\frac{-2+g}{2}=1\]and \[\frac{3+f}{2}=-1\] (By mid point formula) \[\Rightarrow \]\[g=4\]and \[f=-5\] Now, required radius \[=OB=\sqrt{9+16}=\sqrt{25}=5\]
\[{{x}^{2}}+{{y}^{2}}+4x-6y-12=0\] \[\therefore \] \[A=(-2,3)\]and \[B=(g,f)\] Now, from the figure, we have \[\frac{-2+g}{2}=1\]and \[\frac{3+f}{2}=-1\] (By mid point formula) \[\Rightarrow \]\[g=4\]and \[f=-5\] Now, required radius \[=OB=\sqrt{9+16}=\sqrt{25}=5\]
You need to login to perform this action.
You will be redirected in
3 sec
