question_answer

Let Q be the foot of perpendicular from the origin to the plane \[4x-3y+z+13=0\] and R be point (-1, 1, -6) on the plane Then length QR is :     JEE Main  Online Paper (Held On 22 April 2013)

A)  \[\sqrt{14}\]                        

B)  \[\sqrt{\frac{19}{2}}\]

C)  \[3\sqrt{\frac{7}{2}}\]                        

D)  \[\frac{3}{\sqrt{2}}\]

Correct Answer: C

Solution :

 Let P be the image of O in the given plane,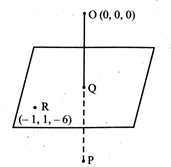 Equation of the plane, \[4x-3y+z+13=0\]OP is normal to the plane, therefore direction ratio of OP are proportional to \[4,-3,1\] Since OP passes through (0, 0, 0) and has direction ratio proportional to \[4,-3,\text{ }1.\] Therefore equation of OP is \[\frac{x-0}{4}=\frac{y-0}{-3}=\frac{z-0}{1}=r\](let) \[\therefore \]   \[x=4r,y=-3r,z=r\] Let the coordinate of P be \[(4r,-3r,r)\] Since Q be the mid point of OP \[\therefore \]  \[Q=\left( 2r,-\frac{3}{2}r,\frac{r}{2} \right)\] Since Q lies in the given plane \[4x-3y+z+13=0\] \[\therefore \]  \[8r+\frac{9}{2}+r+\frac{r}{2}+13=0\] \[\Rightarrow \]               \[r=\frac{-13}{8+\frac{9}{2}+\frac{1}{2}}=\frac{-26}{26}=-1\] \[\therefore \]  \[Q=\left( -2,\frac{3}{2},-\frac{1}{2} \right)\] \[QR=\sqrt{{{(-1+2)}^{2}}+{{\left( 1-\frac{3}{2} \right)}^{2}}+{{\left( -6+\frac{1}{2} \right)}^{2}}}\] \[=\sqrt{1+\frac{1}{4}+\frac{121}{4}}=3\sqrt{\frac{7}{2}}\]