A) \[\frac{{{\operatorname{h}}^{2}}}{2}\sqrt{2}\]
B) \[\frac{{{\operatorname{h}}^{2}}}{2}\]
C) \[\frac{{{\operatorname{h}}^{2}}}{\sqrt{2}}\]
D) \[\frac{{{\operatorname{h}}^{2}}}{4}\]
Correct Answer: D
Solution :
Let base = b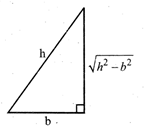 Altitude (or perpendicular) \[=\sqrt{{{h}^{2}}-{{b}^{2}}}\] Area, \[A=\frac{1}{2}\text{ }\!\!\times\!\!\text{ base }\!\!\times\!\!\text{ altitude}\] \[=\frac{1}{2}\times b\times \sqrt{{{h}^{2}}-{{b}^{2}}}\] \[\Rightarrow \] \[\frac{dA}{db}=\frac{1}{2}\left[ \sqrt{{{h}^{2}}-{{b}^{2}}}+b.\frac{-2b}{2\sqrt{{{h}^{2}}-{{b}^{2}}}} \right]\] \[\Rightarrow \] \[=\frac{1}{2}\left[ \frac{{{h}^{2}}-2{{b}^{2}}}{\sqrt{{{h}^{2}}-{{b}^{2}}}} \right]\] Put \[\frac{dA}{db}=0,\]\[\Rightarrow \]\[b=\frac{h}{\sqrt{2}}\] Maximum area \[=\frac{1}{2}\times \frac{h}{\sqrt{2}}\times \sqrt{{{h}^{2}}-\frac{{{h}^{2}}}{2}}=\frac{{{h}^{2}}}{4}\]
Altitude (or perpendicular) \[=\sqrt{{{h}^{2}}-{{b}^{2}}}\] Area, \[A=\frac{1}{2}\text{ }\!\!\times\!\!\text{ base }\!\!\times\!\!\text{ altitude}\] \[=\frac{1}{2}\times b\times \sqrt{{{h}^{2}}-{{b}^{2}}}\] \[\Rightarrow \] \[\frac{dA}{db}=\frac{1}{2}\left[ \sqrt{{{h}^{2}}-{{b}^{2}}}+b.\frac{-2b}{2\sqrt{{{h}^{2}}-{{b}^{2}}}} \right]\] \[\Rightarrow \] \[=\frac{1}{2}\left[ \frac{{{h}^{2}}-2{{b}^{2}}}{\sqrt{{{h}^{2}}-{{b}^{2}}}} \right]\] Put \[\frac{dA}{db}=0,\]\[\Rightarrow \]\[b=\frac{h}{\sqrt{2}}\] Maximum area \[=\frac{1}{2}\times \frac{h}{\sqrt{2}}\times \sqrt{{{h}^{2}}-\frac{{{h}^{2}}}{2}}=\frac{{{h}^{2}}}{4}\]
You need to login to perform this action.
You will be redirected in
3 sec
