question_answer

The locus of the mid-points of the perpendiculars drawn from points on the line, \[x=2y\]to the line \[x=y\] is [JEE MAIN Held on 07-01-2020 Evening]

A) \[5x7y=0\]      

B) \[2x3y=0\]

C) \[3x2y=0\]      

D) \[7x5y=0\]

Correct Answer: A

Solution :

[a] Let coordinate of P is \[(2\lambda ,\lambda )\] and coordinate of mid-point M is\[({{x}_{1}},\text{ }{{y}_{1}})\].

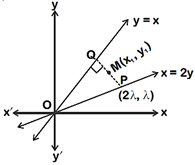\[\therefore \] Coordinate of Q

\[=(2{{x}_{1}}2\lambda ,\text{ }2{{y}_{1}}\lambda )\]

\[\because \] Q lies on line y = x

\[\therefore \,\,\,\lambda \,\,=2{{x}_{1}}2{{y}_{1}}\]                                 ...(i)

(Slope of line PQ) \[\cdot \] (Slope of line y = x) = -1

\[\therefore \,\,\,\frac{\lambda -{{y}_{1}}}{2\lambda -{{x}_{1}}}=-1\]

\[\therefore \,\,\,\lambda =\frac{{{x}_{1}}+{{y}_{1}}}{3}\]                                 ...(ii)

From equation (i) and (ii) : \[5{{x}_{1}}=7{{y}_{1}}\]

\[\therefore \]   Required locus is 5x = 7y.