A) \[\frac{x+3}{3}=\frac{y-5}{1}=\frac{z-2}{-5}\]
B) \[\frac{x+3}{-3}=\frac{y-5}{-1}=\frac{z+2}{5}\]
C) \[\frac{x-3}{3}=\frac{y+5}{1}=\frac{z-2}{-5}\]
D) \[\frac{x-3}{-3}=\frac{y+5}{-1}=\frac{z-2}{5}\]
Correct Answer: A
Solution :
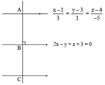 Equation of AB is\[\frac{x-1}{2}=\frac{y-3}{-1}=\frac{z-4}{1}=\lambda \] Co-ordinate of point B is \[\Rightarrow \]\[x=1+2\lambda \]point satisfy the equation of plane \[y=3-\lambda \] \[y=4+\lambda \] \[2(1+2\lambda )-(3-\lambda )+(4+\lambda )+3=0\] \[\Rightarrow \]\[\lambda =-1\] \[\Rightarrow \]Co-ordinate of point B(−1, 4, 3) \[\Rightarrow \]Co-ordinate of point C(−3, 5, 2) \[\Rightarrow \]equation of line passing through ?C? is \[\frac{x+3}{3}=\frac{y-5}{1}=\frac{z-2}{-5}\]
Equation of AB is\[\frac{x-1}{2}=\frac{y-3}{-1}=\frac{z-4}{1}=\lambda \] Co-ordinate of point B is \[\Rightarrow \]\[x=1+2\lambda \]point satisfy the equation of plane \[y=3-\lambda \] \[y=4+\lambda \] \[2(1+2\lambda )-(3-\lambda )+(4+\lambda )+3=0\] \[\Rightarrow \]\[\lambda =-1\] \[\Rightarrow \]Co-ordinate of point B(−1, 4, 3) \[\Rightarrow \]Co-ordinate of point C(−3, 5, 2) \[\Rightarrow \]equation of line passing through ?C? is \[\frac{x+3}{3}=\frac{y-5}{1}=\frac{z-2}{-5}\]
You need to login to perform this action.
You will be redirected in
3 sec
