A) \[\frac{\sqrt{3}}{\sqrt{2}}\]
B) \[\frac{\sqrt{3}}{2}\]
C) \[\frac{1}{2}\]
D) \[\frac{1}{4}\]
Correct Answer: D
Solution :
Equation of C is\[(x-1)2+(y-1)2=1\]?(1) Also let \[(0,y)\equiv (0,k)\] then equation of T is \[{{x}^{2}}+{{(y-k)}^{2}}={{k}^{2}}\] ?(2) From the figure and equations (1) and (2) we get \[{{(1+k)}^{2}}={{1}^{2}}+{{(1-k)}^{2}}\]\[\Rightarrow \]\[k=\frac{1}{4}\] Hence radius of T is\[\frac{1}{4}.\]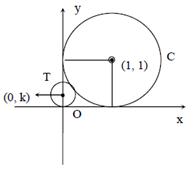
You need to login to perform this action.
You will be redirected in
3 sec
