A) \[\frac{\pi }{2}+\frac{4}{3}\]
B) \[\frac{\pi }{2}-\frac{4}{3}\]
C) \[\frac{\pi }{2}-\frac{2}{3}\]
D) \[\frac{\pi }{2}+\frac{2}{3}\]
Correct Answer: A
Solution :
The required region is The area of region A is \[A=\int\limits_{-1}^{1}{(1-{{y}^{2}})dy=\frac{4}{3}}\]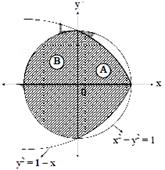 and area of region B is\[B=\frac{\pi }{2}{{(1)}^{2}}=\frac{\pi }{2}\] \[\therefore \]required area\[A+B=\frac{\pi }{2}+\frac{4}{3}\]
and area of region B is\[B=\frac{\pi }{2}{{(1)}^{2}}=\frac{\pi }{2}\] \[\therefore \]required area\[A+B=\frac{\pi }{2}+\frac{4}{3}\]
You need to login to perform this action.
You will be redirected in
3 sec
