question_answer

A block of weight crests on a horizontal floor with coefficient of static friction \[\mu .\]It is desired to make the block move by applying minimum amount offered. The angle \[\theta \] from the horizontal at which the force should be applied and magnitude of the force F are respectively.               [JEE ONLINE 19-05-2012]

A) \[\theta ={{\tan }^{-1}}\left( \mu  \right),F=\frac{\mu W}{\sqrt{1+{{\mu }^{2}}}}\]

B) \[\theta ={{\tan }^{-1}}\left( \frac{1}{\mu } \right),F=\frac{\mu W}{\sqrt{1+{{\mu }^{2}}}}\]

C) \[\theta =0,F=\mu W\]

D) \[\theta ={{\tan }^{-1}}\left( \frac{\mu }{1+\mu } \right),F=\frac{\mu W}{1+\mu }\]

Correct Answer: A

Solution :

[a] Let the force F is applied at an angle \[\theta \] with the horizontal.

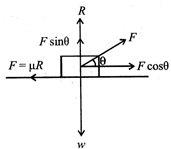For horizontal equilibrium,\[F\cos \theta =\mu R\] (i)

For vertical equilibrium,

\[R+F\sin \theta =mg\]or\[R=mg-F\sin \theta \]       (ii)

Substituting this value of R in eq. (i), we get

\[F\cos \theta =\mu (mg-F\sin \theta )\]

\[=\mu \,mg-\mu \,F\sin \theta \]

or,\[=F(\cos \theta +\mu \sin \theta )=\mu mg\]

or,\[F=\frac{\mu mg}{\cos \theta +\mu \sin \theta }\]                                (iii)

For F to be minimum, the denominator \[(\cos \theta +\mu \sin \theta )\] should be maximum.

\[\therefore \]\[\frac{d}{d\theta }(\cos \theta +\mu \sin \theta )=0\]

or\[-\sin \theta +\mu \cos \theta =0\]or\[\tan \theta =\mu \]

or\[\theta ={{\tan }^{-1}}(\mu )\]

Then, \[\sin \theta =\frac{\mu }{\sqrt{1+{{\mu }^{2}}}}\] and\[\cos \theta =\frac{1}{\sqrt{1+{{\mu }^{2}}}}\]

Hence,\[{{F}_{\min }}\]

\[=\frac{\mu }{\frac{1}{\sqrt{1+{{\mu }^{2}}}}+\frac{1}{\sqrt{1+{{\mu }^{2}}}}}=\frac{\mu w}{\frac{1}{\sqrt{1+{{\mu }^{2}}}}}\]