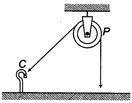
| One end of massless rope, which passes over a massless and frictionless pulley P is tied to a hook C while the other end is free. Maximum tension that the rope can bear is 360 N. With what value of maximum safe acceleration (in \[m{{s}^{-2}}\]) can a man of 60 kg climb on the rope? [AIEEE 2002] |
 |
A) 16
B) 6
C) 4
D) 8
Correct Answer: C
Solution :
| [c] The free body diagram of the person can be drawn as |
| Let the person moves up with an acceleration a, then |
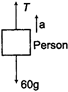 |
| \[T-60g=60a\] |
| \[\Rightarrow \,\,{{a}_{\max }}=\frac{{{T}_{\max }}=-60g}{60}\] |
| \[=\frac{360-60g}{60}=\frac{360-600}{60}=-ve\] |
| which means it is not possible to climb up on the rope. |
| Even in this problem it is not possible to remain at rest on rope. |
 |
| No option is right. |
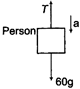
| But if they will ask for the acceleration of climbing down, then \[60g-T=60a\] |
| \[\Rightarrow 60g-{{T}_{\max }}=60{{a}_{\min }}\] |
| \[\therefore \] \[{{a}_{\min }}=\frac{60g-360}{60}=4\,m/{{s}^{2}}\] |
You need to login to perform this action.
You will be redirected in
3 sec
