-
question_answer1) If the lines \[\frac{x+1}{2}=\frac{y-1}{1}=\frac{z+1}{3}\]and \[\frac{x+2}{2}=\frac{y-k}{3}=\frac{z}{3}\] are coplanar, then the value of K is:
JEE Main Online Paper (Held On 09 April 2013)
A)
\[\frac{11}{2}\]
done
clear
B)
\[-\frac{11}{2}\]
done
clear
C)
\[\frac{9}{2}\]
done
clear
D)
\[-\frac{9}{2}\]
done
clear
View Answer play_arrow
-
question_answer2) Statement 1: The slope of the tangent at any point P on parabola, whose axis is the axis of \[x\] and vertex is the origin, is inversely proportional to the ordinate of the point P. Statement 2: The system of parabolas \[{{y}^{2}}=4ax\] satisfies a differential equation of degree 1 and order 1.
JEE Main Online Paper (Held On 09 April 2013)
A)
Statement -1 is true, Statement -2 is true. Statement -2 is correct explanation for statement-1.
done
clear
B)
Statement -1 is true, Statement-2 is true. Statement -2 is not correct explanation for statement-1.
done
clear
C)
Statement -1 is false. Statement-2 is true.
done
clear
D)
Statement -1 is true. Statement-2 is false.
done
clear
E)
Statement -1 is false. Statement-2 is true.
done
clear
View Answer play_arrow
-
question_answer3) If \[{{Z}_{1}}\ne O\] and \[{{Z}_{2}}\] be two complex numbers such that \[\frac{{{Z}_{2}}}{{{Z}_{1}}}\] is a purely imaginary number, then \[\left| \frac{2{{Z}_{1}}+3{{Z}_{2}}}{2{{Z}_{1}}-3{{Z}_{2}}} \right|\] is equal to:
JEE Main Online Paper (Held On 09 April 2013)
A)
2
done
clear
B)
5
done
clear
C)
3
done
clear
D)
1
done
clear
View Answer play_arrow
-
question_answer4) If \[\int{\frac{dx}{x+{{x}^{7}}}=P(x)}\]then,\[\int{\frac{{{x}^{6}}}{x+{{x}^{7}}}=dx}\] is equal to :
JEE Main Online Paper (Held On 09 April 2013)
A)
\[ln\left| x \right|-p(x)+c\]
done
clear
B)
\[ln\left| x \right|+p(x)+c\]
done
clear
C)
\[x-p(x)+c\]
done
clear
D)
\[x+p(x)+c\]
done
clear
View Answer play_arrow
-
question_answer5) If each of the lines \[5x+8y=13\] and \[4x-y=13\]contains a diameter of the circle \[{{x}^{2}}+{{y}^{2}}-2({{a}^{2}}-7+11)x-2({{a}^{2}}-6a+6)y\]\[+{{b}^{3}}+1=0,\] then:
JEE Main Online Paper (Held On 09 April 2013)
A)
\[a=5\] and \[b\notin (-1,1)\]
done
clear
B)
\[a=1\] and \[b\notin (-1,1)\]
done
clear
C)
\[a=2\] and \[b\notin (-\infty ,1)\]
done
clear
D)
\[a=5\] and \[b\in (-\infty ,1)\]
done
clear
View Answer play_arrow
-
question_answer6) If a, b, c, are sides of a scalene triangle, then the value of\[\left| \begin{matrix} a & b & c \\ b & c & a \\ c & a & b \\ \end{matrix} \right|\]is:
JEE Main Online Paper (Held On 09 April 2013)
A)
non negative
done
clear
B)
negative
done
clear
C)
positive
done
clear
D)
non-positive
done
clear
View Answer play_arrow
-
question_answer7) If \[x=\int\limits_{0}^{y}{\frac{dt}{1+{{t}^{2}}},}\] then \[\frac{{{d}^{2}}y}{d{{x}^{2}}}\] is equal to:
JEE Main Online Paper (Held On 09 April 2013)
A)
\[y\]
done
clear
B)
\[\sqrt{1+{{y}^{2}}}\]
done
clear
C)
\[\frac{y}{\sqrt{1+{{y}^{2}}}}\]
done
clear
D)
\[{{y}^{2}}\]
done
clear
View Answer play_arrow
-
question_answer8) Let\[{{a}_{1}},\,\,{{a}_{2}},\,\,{{a}_{3}},..\] be an A.P. such that\[\frac{{{a}_{1}}+{{a}_{2}}+...+{{a}_{p}}}{{{a}_{1}}+{{a}_{2}}+{{a}_{3}}....+{{a}_{q}}}=\frac{{{\operatorname{p}}^{3}}}{{{\operatorname{q}}^{3}}};p\ne q\]. Then\[\frac{{{a}_{6}}}{{{a}_{21}}}\] is equal to:
JEE Main Online Paper (Held On 09 April 2013)
A)
\[\frac{41}{11}\]
done
clear
B)
\[\frac{121}{1681}\]
done
clear
C)
\[\frac{11}{41}\]
done
clear
D)
\[\frac{121}{1861}\]
done
clear
View Answer play_arrow
-
question_answer9) Statement 1: The equation \[x\log x=2-x\] is satisfied by least one value of \[x\] lying between 1 and 2. Statement 2: The function \[f(x)\]= \[x\log x\] is an increasing function is \[[1,2]\] and \[g(x)=2-x\]is a decreasing function in [1,2] and the graphs represented by these functions intersect at a point in [1,2].
JEE Main Online Paper (Held On 09 April 2013)
A)
Statement -1 is true, Statement-2 is true. Statement -2 is correct explanation for statement-1.
done
clear
B)
Statement -1 is true, Statement -2 is true. Statement -2 is not correct explanation for statement-1.
done
clear
C)
Statement -1 is false. Statement-2 is true.
done
clear
D)
Statement -1 is true. Statement-2 is false.
done
clear
View Answer play_arrow
-
question_answer10) Let \[\overset{\to }{\mathop{a}}\,=2\hat{i}-\hat{j}+k,\overset{\to }{\mathop{b}}\,=\hat{i}+2\hat{j}-\hat{k}\]and \[\overset{\to }{\mathop{c}}\,=\hat{i}+\hat{j}-2\overset{\to }{\mathop{k}}\,\]be three vectors. A vector of the type \[\overset{\to }{\mathop{b}}\,+\lambda \overset{\to }{\mathop{c}}\,\] for some scalar\[\lambda ,\] whose projection on \[\overset{\to }{\mathop{a}}\,\] is of magnitude\[\sqrt{\frac{2}{3}},\] is:
JEE Main Online Paper (Held On 09 April 2013)
A)
\[2\hat{i}+\hat{j}+5\hat{k}\]
done
clear
B)
\[2\hat{i}+3\hat{j}-3\hat{k}\]
done
clear
C)
\[2\hat{i}-\hat{j}+5\hat{k}\]
done
clear
D)
\[2\hat{i}+3\hat{j}+3\hat{k}\]
done
clear
View Answer play_arrow
-
question_answer11) The area bounded by the curve \[y=\ln (x)\]and the lines \[y=0,\]\[y=\ln (3)\] and \[x=0\]is equal to:
JEE Main Online Paper (Held On 09 April 2013)
A)
3
done
clear
B)
\[3\,\ln (3)-2\]
done
clear
C)
\[3\,\,\ln (3)+2\]
done
clear
D)
2
done
clear
View Answer play_arrow
-
question_answer12) The Values of ?a? for which one root of the equation \[{{x}^{2}}-(a+1)x+{{a}^{2}}+a-8=0\]exceeds 2 and the other is lesser than 2, are given by:
JEE Main Online Paper (Held On 09 April 2013)
A)
\[3<a<10\]
done
clear
B)
\[a\ge 10\]
done
clear
C)
\[-2<a<3\]
done
clear
D)
(d) \[a\le -2\]
done
clear
View Answer play_arrow
-
question_answer13) If the surface area of a sphere of radius r is increasing uniformly at the rate \[8{{\operatorname{cm}}^{2}}/s,\]then the rate of change of its volume is:
JEE Main Online Paper (Held On 09 April 2013)
A)
constant
done
clear
B)
proportional to \[\sqrt{r}\]
done
clear
C)
proportional to \[{{r}^{2}}\]
done
clear
D)
proportional to \[r\]
done
clear
View Answer play_arrow
-
question_answer14) The probability of a man hitting a target is \[\frac{2}{5}.\] He fires at the target k times (k, a given number). Then the minimum k, so that once is more than \[\frac{7}{10},\] is :
JEE Main Online Paper (Held On 09 April 2013)
A)
3
done
clear
B)
5
done
clear
C)
2
done
clear
D)
4
done
clear
View Answer play_arrow
-
question_answer15) Equation of the line passing though the points of intersection of parabola \[{{x}^{2}}=8y\] and the ellipse\[\frac{{{x}^{2}}}{3}+{{y}^{2}}=1\] is:
JEE Main Online Paper (Held On 09 April 2013)
A)
\[y-3=0\]
done
clear
B)
\[y+3=0\]
done
clear
C)
\[3y+1=0\]
done
clear
D)
\[3y-1=0\]
done
clear
View Answer play_arrow
-
question_answer16) The sum of the series: \[1+\frac{1}{1+2}+\frac{1}{1+2+3}+...........\] up to 10 terms, is:
JEE Main Online Paper (Held On 09 April 2013)
A)
\[\frac{18}{11}\]
done
clear
B)
\[\frac{22}{13}\]
done
clear
C)
\[\frac{20}{11}\]
done
clear
D)
\[\frac{16}{9}\]
done
clear
View Answer play_arrow
-
question_answer17) A value of \[x\] for which \[\sin ({{\cot }^{-1}}(1+x))=\cos ({{\tan }^{-1}}x),\] is:
JEE Main Online Paper (Held On 09 April 2013)
A)
\[-\frac{1}{2}\]
done
clear
B)
1
done
clear
C)
0
done
clear
D)
\[\frac{1}{2}\]
done
clear
View Answer play_arrow
-
question_answer18) If a and c are positive real numbers and the ellipse\[\frac{{{x}^{2}}}{4{{c}^{2}}}+\frac{{{y}^{3}}}{{{c}^{2}}}=1\]has four distinct points in common with the circle \[{{x}^{2}}+{{y}^{2}}=9{{a}^{2}},\] then
JEE Main Online Paper (Held On 09 April 2013)
A)
\[9a-9{{a}^{2}}-2{{c}^{2}}<0\]
done
clear
B)
\[6ac+9{{a}^{2}}-2{{c}^{2}}<0\]
done
clear
C)
\[9ac-9{{a}^{2}}-2{{c}^{2}}>0\]
done
clear
D)
\[6ac+9{{a}^{2}}-2{{c}^{2}}>0\]
done
clear
View Answer play_arrow
-
question_answer19) The vector \[\left( \hat{i}\times \overset{\to }{\mathop{a}}\,.\overset{\to }{\mathop{b}}\, \right)\hat{i}+\left( \hat{j}\times \overset{\to }{\mathop{a}}\,.\overset{\to }{\mathop{b}}\, \right)\hat{j}+(\hat{k}\times \overset{\to }{\mathop{a.}}\,\overset{\to }{\mathop{b}}\,)\hat{j}\] \[+(\hat{k}\times \overset{\to }{\mathop{a}}\,.\overset{\to }{\mathop{b}}\,)\hat{k}\] is equal to
JEE Main Online Paper (Held On 09 April 2013)
A)
\[\vec{b}\times \vec{a}\]
done
clear
B)
\[\overset{\to }{\mathop{a}}\,\]
done
clear
C)
\[\overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\,\]
done
clear
D)
\[\overset{\to }{\mathop{b}}\,\]
done
clear
View Answer play_arrow
-
question_answer20) A light ray emerging from the point source placed at P(1, 3) is reflected at a point Q in the axis of \[x\]. If the reflected ray passes through the point R(6,7), then the abscissa of is:
JEE Main Online Paper (Held On 09 April 2013)
A)
1
done
clear
B)
3
done
clear
C)
\[\frac{7}{2}\]
done
clear
D)
\[\frac{5}{2}\]
done
clear
View Answer play_arrow
-
question_answer21) The mean of a data set consisting of 20 observations is 40. If one observation 53 was wrongly recorded as 33, then the correct mean will be:
JEE Main Online Paper (Held On 09 April 2013)
A)
41
done
clear
B)
49
done
clear
C)
40.5
done
clear
D)
42.5
done
clear
View Answer play_arrow
-
question_answer22)
Let A = {1, 2, 3, 4} and 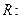
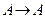 be the relation defined by : R = {(1, 1), (2, 3), (3, 4), (4, 2)}. The correct statement is:
JEE Main Online Paper (Held On 09 April 2013)
be the relation defined by : R = {(1, 1), (2, 3), (3, 4), (4, 2)}. The correct statement is:
JEE Main Online Paper (Held On 09 April 2013)
A)
R does not have an inverse.
done
clear
B)
R is not a one to one function.
done
clear
C)
R is an onto function.
done
clear
D)
R is not a function
done
clear
View Answer play_arrow
-
question_answer23) If the there lines \[x-3y=p,ax+2y=q\]and \[ax+y=r\] form a right - angled triangle then:
JEE Main Online Paper (Held On 09 April 2013)
A)
\[{{a}^{2}}-9a+18=0\]
done
clear
B)
\[{{a}^{2}}-6a-12=0\]
done
clear
C)
\[{{a}^{2}}-6a-18=0\]
done
clear
D)
\[{{a}^{2}}-9a+12=0\]
done
clear
View Answer play_arrow
-
question_answer24) The matrix\[{{A}^{2}}+4A-5I,\]where \[I\]is identity matrix and \[A=\left[ \begin{matrix} 1 & 2 \\ 4 & -3 \\ \end{matrix} \right]\], equals:
JEE Main Online Paper (Held On 09 April 2013)
A)
\[4\left[ \begin{matrix} 2 & 1 \\ 2 & 0 \\ \end{matrix} \right]\]
done
clear
B)
\[4\left[ \begin{matrix} 0 & -1 \\ 2 & 2 \\ \end{matrix} \right]\]
done
clear
C)
\[32\left[ \begin{matrix} 2 & 1 \\ 2 & 0 \\ \end{matrix} \right]\]
done
clear
D)
\[32\left[ \begin{matrix} 1 & 1 \\ 1 & 0 \\ \end{matrix} \right]\]
done
clear
View Answer play_arrow
-
question_answer25) The ratio of the coefficient of \[{{x}^{15}}\] to the term in dependent of \[x\] in the expansion of\[{{\left( {{x}^{2}}+\frac{2}{x} \right)}^{15}}\] is:
JEE Main Online Paper (Held On 09 April 2013)
A)
7 : 16
done
clear
B)
7 : 64
done
clear
C)
1 : 4
done
clear
D)
1 : 32
done
clear
View Answer play_arrow
-
question_answer26) The value of \[\operatorname{l}\underset{x\to 0}{\mathop{im}}\,\frac{1}{x}\left[ {{\tan }^{-1}}\left( \frac{x+1}{2x+1} \right)-\frac{\pi }{4} \right]\]is :
JEE Main Online Paper (Held On 09 April 2013)
A)
1
done
clear
B)
\[-\frac{1}{2}\]
done
clear
C)
2
done
clear
D)
0
done
clear
View Answer play_arrow
-
question_answer27) A vector\[\overset{\to }{\mathop{\operatorname{n}}}\,\] is inclined to \[x-\]axis at\[{{45}^{0}}\], to\[y-\]axis at \[{{60}^{0}}\] and at an acute angle to\[z-\]axis.\[\operatorname{If}\]\[\overset{\to }{\mathop{\operatorname{n}}}\,\] is a normal to a plane passing through the point \[(\sqrt{2},-1,1),\] then the equation of the plane is :
JEE Main Online Paper (Held On 09 April 2013)
A)
\[4\sqrt{2}x+7y+z=2\]
done
clear
B)
\[\sqrt{2}x+y+z=2\]
done
clear
C)
\[3\sqrt{2}x-4y-3z=7\]
done
clear
D)
\[\sqrt{2}x-y-z=2\]
done
clear
View Answer play_arrow
-
question_answer28) Statement 1: The statement \[\operatorname{A}\to (\operatorname{B}\to \operatorname{A})\] is equivalent to \[\operatorname{A}\to \]\[\left( \text{A}\wedge \text{B} \right).\] Statement 2: The statement \[\Rightarrow \]\[\tilde{\ }\left[ \left( \text{A}\wedge \text{B} \right)\to \left( \text{ }\!\!\tilde{\ }\!\!\text{ A}\vee \text{B} \right) \right]\] is a Tautology.
JEE Main Online Paper (Held On 09 April 2013)
A)
Statement -1 is false. Statement -2 is true.
done
clear
B)
Statement -1 is true, Statement-2 is true. Statement -2 is not correct explanation for statement-1.
done
clear
C)
Statement -1 is true, Statement-2 is true. Statement -2 is correct explanation for statement-1.
done
clear
D)
Statement -1 is true. Statement-2 is false.
done
clear
View Answer play_arrow
-
question_answer29) A committee of 4 persons is to formed from 2ladies, 2 old men and 4 young men such that it includes at least 1 lady, at lest 1 old man and at most 2 young men. Then the total number of ways in which this committee can be formed is:
JEE Main Online Paper (Held On 09 April 2013)
A)
40
done
clear
B)
41
done
clear
C)
16
done
clear
D)
32
done
clear
View Answer play_arrow
-
question_answer30) Let\[f(x)=\frac{{{x}^{2}}-x}{{{x}^{2}}+2x},x\ne 0,-2.\]Then\[\frac{d}{dx}\left[ {{f}^{-1}}(x) \right]\] (wherever it is defined) is equal to :
JEE Main Online Paper (Held On 09 April 2013)
A)
frac{-1}{{{(1-x)}^{2}}}\]
done
clear
B)
\[\frac{3}{{{(1-x)}^{2}}}\]
done
clear
C)
\[\frac{1}{{{(1-x)}^{2}}}\]
done
clear
D)
\[\frac{-3}{{{(1-x)}^{2}}}\]
done
clear
View Answer play_arrow
