question_answer

The complex number\[z=x+iy\]which satisfy the equation\[\left| \frac{z-5i}{z+5i} \right|=1\], lie on

A)  the x-axis

B)  the straight line\[y=5\]

C)  a circle passing through the origin

D)  None of the above

Correct Answer: A

Solution :

\[\left| \frac{z-5i}{z+5i} \right|=1\]   \[\Rightarrow \]   \[|z-5i|\,\,=\,\,|z+5i|\] \[\left( \begin{align}   & \text{Using}\,\,\text{definition}\,\,|z-{{z}_{1}}|\,\,=\,\,|z-{{z}_{2}}|\,\,\text{gives} \\  & \text{Perpendicular}\,\,\text{bisector}\,\,\text{of}\,\,{{z}_{1}}\,\,and\,\,{{z}_{2}}. \\ \end{align} \right)\]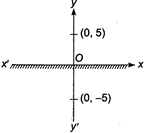 \[\Rightarrow \]               Perpendicular bisector of points (0, 5) and (0, -5). which lies on y-axis.