question_answer

A ship A is moving Westwards with a speed of \[10\,km\,{{h}^{-1}}\] and a ship B 100 km South of A, is moving Northwards with a speed of \[10\,km\,{{h}^{-1}}\]. The time after which the distance between them becomes shortest is  [NEET 2015 ]

A) 0 h       

B) 5 h

C) \[5\sqrt{2}h\]

D) \[10\sqrt{2}h\]

Correct Answer: B

Solution :

It is clear from the diagram that the shortest distance between the ship A and B is PQ.

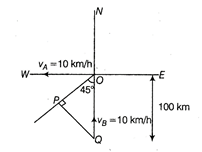Here       \[\sin {{45}^{{}^\circ }}=\frac{PQ}{OQ}\]

\[\Rightarrow \]   \[PQ=100\times \frac{1}{\sqrt{2}}=50\sqrt{2}m\]

Also,

\[{{v}_{AB}}=\sqrt{v_{A}^{2}+v_{B}^{2}}=\sqrt{{{10}^{2}}+{{10}^{2}}}=10\sqrt{2}km/h\]

So, time taken for them to reach shortest path is

\[t=\frac{PQ}{{{v}_{AB}}}=\frac{50\sqrt{2}}{10\sqrt{2}}=5h\]