question_answer

When an object is shot from the bottom of a long smooth inclined plane kept at an angle\[60{}^\circ \] with horizontal, it can travel a distance \[{{x}_{1}}\]along the plane. But when the inclination is decreased to \[30{}^\circ \] and the same object is shot with the same velocity, it can travel \[{{x}_{2}}\]distance. Then \[{{x}_{1}}:{{x}_{2}}\]will be:                                         [NEET 5-5-2019]

A) \[1:\sqrt{3}\]

B) \[1:2\sqrt{3}\]

C) \[1:\sqrt{2}\]                 

D) \[\sqrt{2}:1\]

Correct Answer: A

Solution :

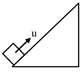            \[{{v}^{2}}={{u}^{2}}+2as\] \[0={{u}^{2}}2g\text{ }sin\theta S\] \[S=\frac{{{u}^{2}}}{2g\sin \theta }\] \[S\propto \frac{1}{\sin \theta }\] \[\frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{\sin }_{2}}\theta }{{{\sin }_{1}}\theta }=\frac{\sin 30{}^\circ }{\sin 60{}^\circ }=\frac{1}{\sqrt{3}}\]