question_answer

In figure 3, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If \[\angle PRQ=120{}^\circ \], then prove that, \[OR=PR+RQ\].

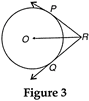Answer:

O is the centre of the circle and \[\angle PRQ=120{}^\circ \]

Construction: Join \[OP,OQ\]

To prove: \[OP=PR+RQ\]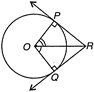

Proof: We know that,

Tangent to a circle is perpendicular to the radius at the point of tangent i.e., \[OP\bot RP\] and \[OQ\bot RQ\].

\[\therefore \angle OPR=\angle OQR=90{}^\circ \]

Now, in \[\Delta \,OPR\] and \[\Delta \,OQR\],

\[OP=OQ\]                         [Radius of circle]

\[OR=OR\]             [Common]

\[\angle OPR=\angle OQR=90{}^\circ \]              [Each\[90{}^\circ \]]

\[\therefore \Delta \,OPR\cong \Delta \,OQR\]          [By SSA congruence]

So,                   \[PR=QR\]                     [By c.p.c.t.]

and                   \[\angle ORP=\angle ORQ\]

\[=\frac{120{}^\circ }{2}=60{}^\circ \]

Now, in \[\Delta \,OPR\]

\[\cos \,\,60{}^\circ =\frac{PR}{OR}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ \because \,\cos \theta =\frac{\text{Base}}{\text{Hypotenuse}} \right]\]

\[\frac{1}{2}=\frac{PR}{OQ}\]

\[OR=2PR\]

\[OR=PR+PR\]

\[OR=PR+RQ\]              \[[\because \,PR=RQ]\]

Hence,              \[OR=PR+RQ\]              Hence Proved.