question_answer

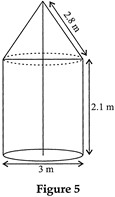
In fig. 5, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3 m respectively and the slant height of conical part is 2.8 m, find the cost of canvas needed to make the tent if the canvas is available at the rate of Rs. 500/sq. metre. (Use \[\pi =\frac{22}{7}\] )

Answer:

We have, height (h) and diameter (d) of cylinder as \[2.1\text{ }m\] and \[3\text{ }m\] respectively and slant height of conical part is \[2.5\text{ }m\].

Area of Canvas needed = C.S.A. of (cylinder + cone)

\[=2\pi rh+\pi rl\]

\[=2\times \frac{22}{7}\times \frac{3}{4}\times 2.1+\frac{22}{7}\times \frac{3}{2}\times 2.8\]

\[=\frac{22}{7}(6.3+4.2)\]

\[=\frac{22}{7}\times 10.5=33\,{{m}^{2}}\]

\[\therefore \] Cost of canvas needed at the rate of Rs. \[500/{{m}^{2}}\]

\[=Rs.(33\times 500)=Rs.\,16500\]