question_answer

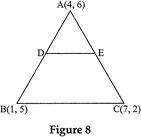
In fig. 8, the vertices of \[\Delta \,ABC\] are \[A(4,6),\,\,B(1,5)\]and \[C(7,2)\]. A line ? segment DE is drawn to intersect the sides AB and AC at D and E respectively such that \[\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{3}\]. Calculate the area of \[\Delta \,ADE\] and compare it with area of \[\Delta \,ABC\].

Answer:

We have, the vertices of \[\Delta \text{ }ABC\] as \[A(4,6),\,\,B(1,5)\] and \[C(7,2)\]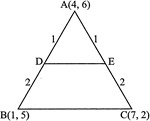

And \[\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{3}\]

Then, coordinated of D are

\[\left( \frac{1(1)+2(4)}{1+2},\frac{1(5)+2(6)}{1+2} \right)\]

\[\left( \frac{1+8}{3},\frac{5+12}{3} \right)\,i.e.,\,\,D\left( 3,\frac{17}{3} \right)\]

And coordinates of E are

\[\left( \frac{1(7)+2(4)}{1+2},\frac{1(2)+2(6)}{1+2} \right)\]

\[\left( \frac{7+8}{3},\frac{2+12}{3} \right)\,\,i.e.,\,\,E\left( 5,\frac{14}{3} \right)\]

Now, Area of \[\Delta \,ADE\]

\[=\frac{1}{2}\left[ 4\left( \frac{17}{3}-\frac{14}{3} \right)+3\left( \frac{14}{3}-6 \right)+5\left( 6-\frac{17}{3} \right) \right]\]

\[=\frac{1}{2}\left[ 4(1)+3\left( -\frac{4}{3} \right)+5\left( \frac{1}{3} \right) \right]\]

\[=\frac{5}{6}\] units

And Area of \[\Delta \,ABC\]

\[=\frac{1}{2}[4(5-2)+1(2-6)+7(6-5)]\]

\[=\frac{1}{2}[4(3)+1(-4)+7(1)]=\frac{15}{2}\] units.

\[\therefore \,\,\frac{ar\,(\Delta \,ADE)}{ar(\Delta \,ABC)}=\frac{5/6}{15/2}=\frac{1}{9}\]

i.e., \[ar\,(\Delta \,ADE):ar\,(\Delta \,ABC)=1:9\]