question_answer

An observer finds the angle of elevation of the top of the tower from a certain point on the ground as \[30{}^\circ \]. If the observer moves \[20\text{ }m\] towards the base of the tower, the angle of elevation of the top increases by \[15{}^\circ \], find the height of the tower.

Answer:

Let AB be tower of height h

From \[\Delta \,ABC,\frac{AB}{BC}=\tan \,\,45{}^\circ \]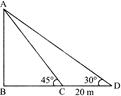

\[h=BC\]

From \[\Delta \,\,ABD,\frac{AB}{BD}=\tan \,\,30{}^\circ \]

\[h=\frac{BD}{\sqrt{3}}\] or \[BD=\sqrt{3}\,h\]

\[CD=BD-BC\]

\[\Rightarrow \]               \[=\sqrt{3}\,h-h=\left( \sqrt{3}-1 \right)h\]

\[\Rightarrow \]               \[20\,m=\left( \sqrt{3}-1 \right)h\]

\[\Rightarrow \]               \[h=\frac{20}{\sqrt{3}-1}\times \frac{\sqrt{3}+1}{\sqrt{3}+1}=\frac{20\left( \sqrt{3}+1 \right)}{{{\left( \sqrt{3} \right)}^{2}}-{{(1)}^{2}}}\]

\[=\frac{20\left( \sqrt{3}+1 \right)}{2}=10\left( \sqrt{3}+1 \right)m\]