question_answer

If \[A\,(-2,1,)\text{ }B\,(a,0,\text{ }C\text{ (}4,b)\] and \[D\text{ (}1,2)\] are the vertices of a parallelogram ABCD, find the values of a and b. Hence find the lengths of its sides.

OR

If \[A\,(-5,7),\text{ }B\,(-4,-5),\text{ }C\text{ (}-1,-6)\] and \[D\text{ (}4,5)\]are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.

Answer:

Given, ABCD is a parallelogram.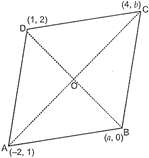

Midpoint of \[AC=\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]

\[=\left( \frac{-2+4}{2},\frac{1+b}{2} \right)\]

\[=\left( \frac{2}{2},\frac{1+b}{2} \right)\]

\[=\left( 1,\frac{1+b}{2} \right)\]

Midpoint of \[BD=\left( \frac{x{{'}_{1}}+x{{'}_{2}}}{2},\frac{y{{'}_{1}}+y{{'}_{2}}}{2} \right)\]

\[=\left( \frac{a+1}{2},\frac{0+2}{2} \right)\]

\[=\left( \frac{a+1}{2},\frac{2}{2} \right)\]

\[=\left( \frac{a+1}{2},1 \right)\]

Since, diagonals of a parallelogram bisect each other,

\[\therefore \]                  \[\left( 1,\frac{1+b}{2} \right)=\left( \frac{a+1}{2},1 \right)\]

On comparing, we get

\[\therefore \]      \[\frac{a+1}{2}=1\]                  \[\frac{1+b}{2}=1\]

\[\Rightarrow \]   \[a+1=2\]         \[\Rightarrow \]   \[1+b=2\]

\[\Rightarrow \]   \[a=1\]              \[\Rightarrow \]        \[b=1\]

Therefore, the coordinates of vertices of parallelogram ABCD are \[A\,(-2,1),\text{ }B\,(1,0),\,\,C\,(4,1)\]and \[D\,(1,2)\]Length of side

\[AB=DC=\sqrt{{{(1+2)}^{2}}+{{(0-1)}^{2}}}\]

\[=\sqrt{9+1}=\sqrt{10}\] units

And,     \[AD=BC=\sqrt{{{(1+2)}^{2}}+{{(2-1)}^{2}}}\]

\[=\sqrt{9+1}=\sqrt{10}\] units

OR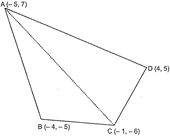

Given ABCD is quadrilateral.

By joining points A and C, the quadrilateral is divided into two triangles.

Now, Area of quad. ABCD = Area of \[\Delta ABC\]+ Area of \[\Delta \,ACD\]

Area of \[\Delta \text{ }ABC\]

\[=\frac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]\]

\[=\frac{1}{2}\left[ -5\left( -5+6 \right)-4\left( -6-7 \right)-1\left( 7+5 \right) \right]\]

\[=\frac{1}{2}[-5(1)-4(-13)-1(12)]\]

\[=\frac{1}{2}(-5+52-12)\]

\[=\frac{1}{2}(35)=\frac{35}{2}\] sq. units.

Area of \[\Delta \text{ }ADC\]

\[=\frac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]\]

\[=\frac{1}{2}[-5(5+6)+4(-6-7)+(-1)(7-5)]\]

\[=\frac{1}{2}[-5(11)+4(-13)-1(2)]\]

\[=\frac{1}{2}(-55+52-12)\]

\[=\frac{1}{2}|-109|=\frac{109}{2}\] sq. units.

Area of quadrilateral ABCD

\[=\frac{35}{2}+\frac{109}{2}\]

\[=\frac{144}{2}=72\] sq. units.