Answer:
Here, \[p\left( x \right)=2{{x}^{4}}-9{{x}^{3}}+5{{x}^{2}}+3x-1\] And two of its zeroes are \[\left( 2+\sqrt{3} \right)\] and \[\left( 2-\sqrt{3} \right)\] Quadratic polynomial with zeroes is given by, \[\left\{ x-\left( 2+\sqrt{3} \right) \right\}.\left\{ x-\left( 2-\sqrt{3} \right) \right\}\] \[\Rightarrow \] \[\left( x-2-\sqrt{3} \right)\left( x-2+\sqrt{3} \right)\] \[\Rightarrow \] \[{{(x-2)}^{2}}-{{(\sqrt{3})}^{2}}\] \[\Rightarrow \] \[{{x}^{2}}-4x+4-3\] \[\Rightarrow \] \[{{x}^{2}}-4x+1=g(x)\] (say) Now, g (x) will be a factor of p(x) so g (x) will be divisible by p (x) 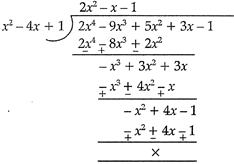
For other zeroes, \[2{{x}^{2}}-x-1=0\] \[2{{x}^{2}}-2x+x-1=0\] or \[2x(x-1)+1\text{ (}x-1)=0\] \[(x-1)(2x+1)=0\] \[x-1=0\,\,\,\,2x+1=0\] \[x=1,x=\frac{-1}{2}\] Zeroes of p(x) are \[1,\frac{-1}{2},2+\sqrt{3}\] and \[2-\sqrt{3}\].
You need to login to perform this action.
You will be redirected in
3 sec
