| Analyse the following observation table showing variation of image distance \[\mathbf{(v)}\] with object distance \[\mathbf{(u)}\] in case of a convex lens and answer the questions that follow, without doing any calculations: | ||
| S. No. | Object distance u(cm) | Image distance v(cm) |
| 1. | \[-90\] | \[+18\] |
| 2. | \[-60\] | \[+20\] |
| 3. | \[-30\] | \[+30\] |
| 4. | \[-20\] | \[+60\] |
| 5. | \[-18\] | \[+90\] |
| 6. | \[-10\] | \[+100\] |
| (a) What is the focal length of the convex lens? Give reason in support of your answer. | ||
| (b) Write the serial number of that observation which is not correct. How did you arrive at this conclusion? | ||
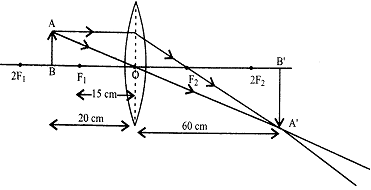
| (c) Take an appropriate scale to draw ray diagram for the observation at S. No. 4 and find the approximate value of magnification. | ||
Answer:
(a) From S. No. 3, we can say that the radius of curvature is 30 cm because when an object is placed at the centre of curvature of a convex lens, its image is formed on the other side of the lens at the same distance from the lens. And, we also know that focal length is half of the radius of curvature. Therefore, focal length of the lens is +15 cm.
(b) S. No. 6 is not correct as the object distance is between focus and optical centre, and in such cases, the image formed is always virtual. But in this case, a real image is formed as the image distance is positive.
(c) Approximate value of magnification for object distance \[-20\]cm and image distance + 60 cm is\[-3\].
You need to login to perform this action.
You will be redirected in
3 sec
