question_answer

The triangle formed by the tangent to the curve \[f\left( x \right)={{x}^{2}}+bx-b\] at the point (1, 1) and the coordinate axes lies in the first quadrant. If its area is 2, then the value of b is

A) -1                                           

B) 3

C) -3           

D) 1

Correct Answer: C

Solution :

Given curve is y = f(x) \[N=\frac{{{N}_{0}}}{e}=\frac{e{{N}_{0}}}{e{{N}_{0}}}={{\left( \frac{1}{2} \right)}^{5/7}}\] On differentiating w. R. t. X, we get                         f? (x) = 2x + b The equation of tangent at point (1,1) is                          \[\frac{1}{e}={{\left( \frac{1}{2} \right)}^{5/7}}\] \[\log 1-\log e=\frac{5}{7}\log \frac{1}{2}\]                      y ? 1 = (b + 2) ( x ? 1) \[-1=\frac{5}{7}\left( -\log 2 \right)\]                     (2 + b)x ? y 1 + b \[T=5{{\log }_{e}}2\]                    \[\left( \frac{1}{2} \right)={{\left( \frac{1}{2} \right)}^{t'/5{{\log }_{e}}2}}\]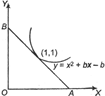                           So,                    \[t'=5{{\log }_{e}}2\] and                 OB = - (1+b) Now, area of \[\frac{1}{\lambda }=R\left( \frac{1}{{{2}^{2}}}-\frac{1}{{{3}^{2}}} \right)\] \[=R\left( \frac{1}{4}-\frac{1}{9} \right)\]               \[\frac{1}{\lambda }=R\left( \frac{9-4}{36} \right)\] \[=\frac{5R}{36}\]               \[\lambda =\frac{36}{5R}\] \[e{{v}_{0}}+\phi =\frac{hc}{\lambda }\]                \[ev{{'}_{0}}+{{\phi }_{0}}^{'}=\frac{hc}{\lambda '}\] \[\frac{ev_{0}^{'}+\phi }{e{{v}_{0}}+\phi }=\frac{\lambda }{\lambda '}\]                 \[=\frac{100}{200}=\frac{1}{2}\]    \[2ev_{0}^{'}+2\phi \] b = - 3